题目内容
| 黄金类别 | 24k | 22k | 18k |
| 密度(×103kg/m3) | 19.26 | 17.65 | 15.15 |
(2)如图甲所示,在已经平衡的天平上,王哲将6.8g的蹦蹦球用线吊入烧杯的水中后,只须将游码从最左端移到如图乙所示的位置,天平重新平衡.则该球的体积是
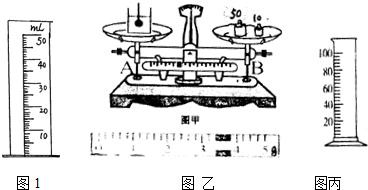
(2)天平原来平衡,现在将蹦蹦球用线吊入烧杯的水中后,蹦蹦球受到水的浮力,同时蹦蹦球给水向下的力,相当于左盘增加了这么重的水;可见天平左盘增加了蹦蹦球排开水的质量,知道只须将游码从最左端移到如图乙所示的位置,天平重新平衡,读出游码示数.可求蹦蹦球排开水的质量,利用密度公式求蹦蹦球的体积,再利用密度公式求蹦蹦球的密度;
图丙的分度值为4mL,根据蹦蹦球的体积判断能否准确测量.
(1)金币的质量m=3.1g,若密度为15.15g/cm3,金币的体积V=
| m |
| ρ |
| 3.1g |
| 15.15g/cm3 |
而量筒的最小刻度值为1mL,所以不能准确测量金币的体积,无法准确测量金币的密度;
(2)将蹦蹦球用线吊入烧杯的水中后,天平左盘增加了蹦蹦球排开水的质量,由图乙可知,m排=3.4g.
蹦蹦球的体积V=V排=
| m排 |
| ρ水 |
| 3.4g |
| 1g/cm3 |
蹦蹦球的密度ρ球=
| m球 |
| ρ球 |
| 6.8g |
| 3.4cm3 |
因为量筒最小分度值为4cm3,小球体积小于分度值,体积测不准确.
故答案为:
(1)不能;黄金体积小于量筒的最小分度值,金币体积无法准确测量;
(2)3.4; 2×103;不同意,量筒最小分度值为4cm3,小球体积小于分度值,体积测不准确.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 量筒的使用
量筒的使用(1)用量筒测不规则固体体积的步骤如下:在量筒中注入适量的水,读出此时水面所对应的示数V1;把固体浸没在盛有适量水的量筒中,读出此时水面所对应的示数V2,则待测固体的体积V=
(2)你认为:在上述操作过程中怎样把握注入量筒内水的多少,才是“适量”的?
答:
(3)小华有一枚质量为3.1g的金币,经查阅资料知,制作金币所用材料的类别及密度如表所示
小华准备用量筒测出该金币的体积,计算出其密度,从而鉴别它的黄金类别.实验时,小华选用了一个能放入该金币的量筒,其规格如图所示.
| 黄金类别 | 24K黄金 | 22K黄金 | 18K黄金 |
| 密度(103kg/m3) | 19.26 | 17.65 | 15.45 |
答:
小华有一枚质量为3.1g的金币,经查阅资料知,制作金币所用材料的类别及密度如下表所示:
| 黄金类别 | 24k | 22k | 18k |
| 密度(×103kg/m3) | 19.26 | 17.65 | 15.15 |
(1)小华准备用量筒测出该金币的体积,计算密度,从而鉴别它的黄金类别,实验时小华选用一个能放入该金币的量筒,规格如图7示,你认为通过上述实验能否鉴别该金币的黄金类别? (能或不能)原因是
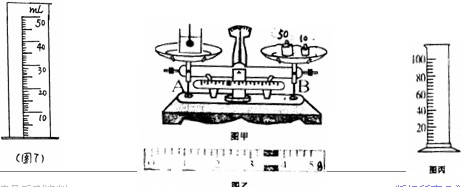
(2)如图甲所示,在已经平衡的天平上,王哲将6.8g的蹦蹦球用线吊入烧杯的水中后,只须将游码从最左端移到如图乙所示的位置,天平重新平衡。则该球的体积是 cm3,密度是 kg/m3。思达同学认为,如果用如图丙所示的量筒来测小球的体积,误差会更小些,你同意他的看法吗?请谈谈你的看法 。(每空1分,共3分)
小华有一枚质量为3.1g的金币,经查阅资料知,制作金币所用材料的类别及密度如下表所示:
|
黄金类别 |
24k |
22k |
18k |
|
密度(×103kg/m3) |
19.26 |
17.65 |
15.15 |
(1)小华准备用量筒测出该金币的体积,计算密度,从而鉴别它的黄金类别,实验时小华选用一个能放入该金币的量筒,规格如图7示,你认为通过上述实验能否鉴别该金币的黄金类别? (能或不能)原因是
(2)如图甲所示,在已经平衡的天平上,王哲将6.8g的蹦蹦球用线吊入烧杯的水中后,只须将游码从最左端移到如图乙所示的位置,天平重新平衡。则该球的体积是 cm3,密度是 kg/m3。思达同学认为,如果用如图丙所示的量筒来测小球的体积,误差会更小些,你同意他的看法吗?请谈谈你的看法 。(每空1分,共3分)
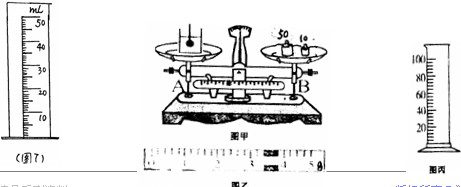
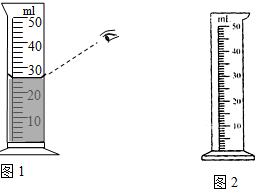 量筒的应用
量筒的应用