题目内容
【题目】小明注意家里摆钟的钟摆在有规律地摆动,经认真观察发现钟摆来回摆动一次的时间刚好是1秒,就想:是不是所有的摆来回摆动一次的时间都是1秒呢?于是,他请教了物理老师,知道摆来回摆动一次的时间叫做周期,在老师的指导下他设计如图2所示的单摆(即细绳下系一小钢球)进行探究.
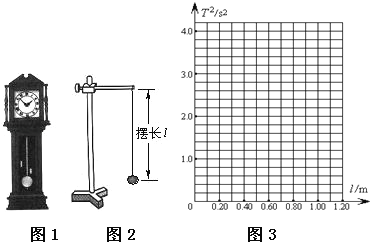
实验数据记录如下表:
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
摆长l/m | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 1.00 |
周期T/s | 1.1 | 1.3 | 1.4 | 1.5 | 1.7 | 1.8 | 1.9 | 2.0 |
周期平方 | 1.2 | 1.6 | 2.0 | 2.3 | 2.9 | 3.2 | 3.6 | 4.0 |
(1)从表中数据可知,单摆的摆长l越长,周期T越 (选填“长”或“短”).
(2)请根据表中数据在图3中作出单摆周期的平方T2与摆长l的关系图象.
(3)分析图3所示图象,可知实验中用的单摆周期的平方T2与l成 关系.
(4)由表中实验记录可知,单摆来回摆动一次时间比较短,直接测量摆动一次的时间误差比较大.你认为小明为了减小测量误差是怎么做的? .
(5)生活中若摆钟走慢了,应如何调整钟摆的长度? .
【答案】(1)长;
(2)
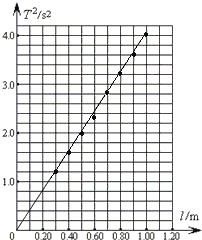
(3)正比;
(4)可测出单摆来回摆动多次(如30次)的时间,再计算出来回摆动1次的时间.
(5)将钟摆的长度调短.
【解析】
试题分析:(1)解决此题的关键是通过分析表格中的周期和摆长数据,看周期随摆长的增大怎样变化;
(2)作图时要先根据数据进行描点,横坐标是摆长,纵坐标是周期的平方,然后用平滑的线连接各点;
(3)解决此题的关键是根据图象的特征判断单摆周期的平方T2与l的关系:
如果图象是一条平滑的直线,说明它们之间是成正比例关系;
如果是双曲线说明它们是成反比例关系;
(4)由于摆动一个周期所需时间很短,可以采用累计法进行分析计算摆动一次所需时间;
(5)可以通过调整摆的长度来调整摆动时间,因为摆长越长,摆动周期越长,摆长越短,摆动周期越短.
解:(1)由表格数据可知,摆长越长,摆动一次所需时间越长;
(2)按照表格中的数据进行描点,作图如下:
(3)做出的图象是直线,说明单摆周期的平方T2与摆长l之间是成正比例关系;
(4)因为单摆摆动一个周期所需时间很短,所以可以采用累计法进行分析计算,可测出单摆来回摆动多次(如30次)的时间,再计算出来回摆动1次的时间;
(5)若摆钟走慢了,说明钟表的摆动周期长了,所以应该将表的摆长调短些;
故答案为:(1)长;
(3)正比;
(4)可测出单摆来回摆动多次(如30次)的时间,再计算出来回摆动1次的时间.
(5)将钟摆的长度调短.