题目内容
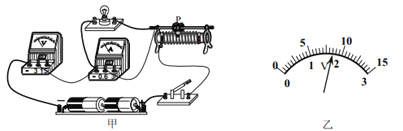
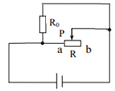
【题目】如图所示,电源电压不变,灯泡L标有“4V 2W”字样,R0的阻值为16Ω。连S2断开、S3闭合,滑片P从b端滑到某一位置时,滑动变阻器R接入电路的电阻减小了8Ω,此过程中电压表的示数由3.2V变为4V。则:
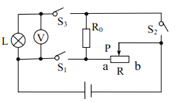
(1)灯泡的电阻为________灯泡正常工作时的电流为________A。
(2)电源电压和滑动变阻器的最大阻值各为多少?(不考虑溫度对灯丝电阻的影响)
(3)当S1、S2闭合、S3断开时,电路消耗的最小功率是多少?(符合电路操作规范要求)
【答案】(1)8;0.5;(2)16Ω.(3)32W
【解析】试题分析:(1)灯泡正常发光时的电压为4V,电功率为2W,
根据P=UI可得,灯泡正常发光时的电流:IL=PL/UL=2W/4V=0.5A,
根据欧姆定律可得,灯泡的电阻:RL =UL/IL=4V/0.5A=8Ω;
(2)当S1 、S2 断开、S3 闭合,等效电路图如图1所示;
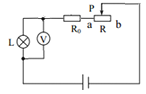
由于滑片P从b端滑到某一位罝时,电压表的示数由3.2V变为4V
则当滑片P在b端时电压表的示数为3.2V,电路中的电流为I1=U1/RL=3.2V/8Ω=0.4A,
根据串联电路的特点和欧姆定律可得:电源电压U=I1(RL+R0+Rab)=0.4A(8Ω+16Ω+Rab) ①
当滑片P在某一位罝时电压表的示数为4V;由于灯泡的实际等于与额定电压相等,
则灯泡正常发光,所以电路中的电流为I2=IL=0.5A,
根据串联电路的特点和欧姆定律可得:电源电压U=I2(RL+R0+R′)=0.5A(8Ω+16Ω+R′) ②
已知Rab-R′=8Ω ③
解①②③联立方程得:Rab=16Ω,R′=8Ω,U=16V;
(3)当S1、S2闭合、S3断开时,等效电路图如图所示;
动变阻器接入电路中的电阻最大时,电路的总功率最小,则I滑=U/Rab=16V/16Ω=1A,I0 =U/R0=16V/16Ω=1A,
所以并联电路中干路电流I=I滑+I0=1A+1A=2A,电路的最小功率:Pmin=UI=16V×2A=32W

 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案