题目内容
 定滑轮在使用时相当于一个杠杆.如图所示,某人用绳子沿着倾斜方向通过定滑轮拉住钩码,已知人手的拉力为F,钩码重力为G
定滑轮在使用时相当于一个杠杆.如图所示,某人用绳子沿着倾斜方向通过定滑轮拉住钩码,已知人手的拉力为F,钩码重力为G(1)请在图中标出这只“杠杆”的支点O,画出拉力F、钩码重力G及它们的力臂(保留作图痕迹):
(2)若不计摩擦和绳重,请用杠杆平衡条件推证:F=G
(3)若实际利用该定滑轮提升重物时,F=1.2G,求机械效率.
分析:(1)在外力作用下,杠杆可以绕某一固定点转动,根据杠杆的定义中的某一固定点确定支点O;手作用在绳子上的力为拉力F,过钩码的重心作竖直向下的力即重力;最后根据力臂的定义画出相应的力臂.
(2)从图中找出动力臂和阻力臂的关系,利用杠杆平衡条件的即可验证拉力和钩码重力的关系.
(3)根据η=
×100%可求得机械效率.
(2)从图中找出动力臂和阻力臂的关系,利用杠杆平衡条件的即可验证拉力和钩码重力的关系.
(3)根据η=
| W有用 |
| W总 |
解答:解:(1)定滑轮可以绕中间轴转动,所以支点O为定滑轮的轴;
拉力是自由端沿绳子斜向下的拉力,过钩码重心作竖直向下的重力;
过支点O分别作动力作用线和阻力作用线的垂线段(即动力臂L2和阻力臂L1).
如图所示:
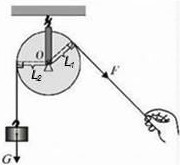
(2)由几何知识知:L1=L2=R(R为滑轮半径)
根据杠杆平衡条件:F1?L1=F2?L2,
即F?L1=G?L2,得:F=G.
(3)已知F=1.2G,h=s,
则η=
×100%=
=
×100%≈83%.
故答案为:(1)如图所示;
(2)见上面证明;
(3)机械效率为83%.
拉力是自由端沿绳子斜向下的拉力,过钩码重心作竖直向下的重力;
过支点O分别作动力作用线和阻力作用线的垂线段(即动力臂L2和阻力臂L1).
如图所示:

(2)由几何知识知:L1=L2=R(R为滑轮半径)
根据杠杆平衡条件:F1?L1=F2?L2,
即F?L1=G?L2,得:F=G.
(3)已知F=1.2G,h=s,
则η=
| W有用 |
| W总 |
| Gh |
| Fs |
| G |
| 1.2G |
故答案为:(1)如图所示;
(2)见上面证明;
(3)机械效率为83%.
点评:此题考查了力的示意图,杠杆的平衡条件,力臂的画法,机械效率的计算等知识点,是一道综合性较强的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 17、定滑轮在使用时相当于一个杠杆.如图所示,某人用绳子沿着倾斜方向通过定滑轮拉住钩码,已知人手的拉力为F,钩码重力为G.
17、定滑轮在使用时相当于一个杠杆.如图所示,某人用绳子沿着倾斜方向通过定滑轮拉住钩码,已知人手的拉力为F,钩码重力为G. (2011?犍为县模拟)定滑轮在使用时相当于一个杠杆.如图所示,某人用绳子沿着倾斜方向通过定滑轮拉住钩码,已知人手的拉力为F,钩码重力为G.请在图中标出这只“杠杆”的支点O,画出拉力F、钩码重力G及它们的力臂(保留作图痕迹)
(2011?犍为县模拟)定滑轮在使用时相当于一个杠杆.如图所示,某人用绳子沿着倾斜方向通过定滑轮拉住钩码,已知人手的拉力为F,钩码重力为G.请在图中标出这只“杠杆”的支点O,画出拉力F、钩码重力G及它们的力臂(保留作图痕迹) 定滑轮在使用时相当于一个
定滑轮在使用时相当于一个