题目内容
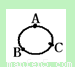
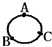 如图所示,一根阻值为R=27Ω的粗细均匀的电阻线弯成一个圆,A、B、C 是三等分点,若将AB接在电源上,此时接入电路中的总电阻是
如图所示,一根阻值为R=27Ω的粗细均匀的电阻线弯成一个圆,A、B、C 是三等分点,若将AB接在电源上,此时接入电路中的总电阻是6Ω
6Ω
.分析:求出AB、BC、CA三段的电阻,AB两点间的电阻为AB段的电阻和ACB段的电阻并联,根据并联电阻的特点(并联电路总电阻的倒数等于各并联电阻的倒数之和)求解.
解答:解:∵R=27Ω,
∴RAC=RBC=RAB=
R=
×27Ω=9Ω,
若将AB接在电源上,是将BC和CA串联后,再和AB并联,
RAB=9Ω,RACB=2×9Ω=18Ω,
∵
=
+
,
∴R并=
=
=6Ω.
故答案为:6Ω.
∴RAC=RBC=RAB=
| 1 |
| 3 |
| 1 |
| 3 |
若将AB接在电源上,是将BC和CA串联后,再和AB并联,
RAB=9Ω,RACB=2×9Ω=18Ω,
∵
| 1 |
| R并 |
| 1 |
| RAB |
| 1 |
| RACB |
∴R并=
| RABRACB |
| RAB+RACB |
| 9Ω×18Ω |
| 9Ω+18Ω |
故答案为:6Ω.
点评:本题考查了电阻并联的计算,能从图看出AB两点间的电阻为两端导线(AB、ACB)并联是本题的关键.

练习册系列答案
相关题目