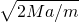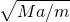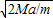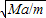题目内容
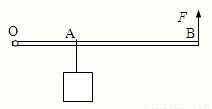
 如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?( )
如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?( )分析:解答本题需要根据杠杆平衡条件F1L1=F2L2去分析计算:
本题中动力为F,动力臂为OB,而阻力有两个(一个是重物Mg,另一个是杠杆本身的重力),所以阻力臂也有两个(重物G的力臂是OA,杠杆重力的力臂是
OB),明确了动力、动力臂、阻力和阻力臂之后,我们就可以根据杠杆平衡条件列出一个方程,然后根据数学方面的知识求解方程.
本题中动力为F,动力臂为OB,而阻力有两个(一个是重物Mg,另一个是杠杆本身的重力),所以阻力臂也有两个(重物G的力臂是OA,杠杆重力的力臂是
| 1 |
| 2 |
解答:解:(1)由题意可知,杠杆的动力为F,动力臂为OB,阻力分别是重物G物和杠杆的重力G杠杆,阻力臂分别是OA和
OB,重物的重力G物=Mg
杠杆的重力G杠杆=mg×OB,
由杠杆平衡条件F1L1=F2L2可得:
F?OB=G物?OA+G杠杆?
OB,
(2)代入相关数据:
则F?OB=Mg?a+mg?OB?
OB,
得:F?OB=Mga+
mg?(OB)2,
移项得:
mg?(OB)2-F?OB+Mga=0,
∵杠杆的长度OB是确定的,只有一个,所以该方程只能取一个解,
∴该方程根的判别式b2-4ac等于0,因为当b2-4ac=0时,方程有两个相等的实数根,即有一个解,
即:则F2-4×
mg×Mga=0,
则F2=2mMg2a,
得F=
?g,
(3)将F=
?g代入方程
mg?(OB)2-F?OB+Mga=0,
解得OB=
.
故选A.
| 1 |
| 2 |
杠杆的重力G杠杆=mg×OB,
由杠杆平衡条件F1L1=F2L2可得:
F?OB=G物?OA+G杠杆?
| 1 |
| 2 |
(2)代入相关数据:
则F?OB=Mg?a+mg?OB?
| 1 |
| 2 |
得:F?OB=Mga+
| 1 |
| 2 |
移项得:
| 1 |
| 2 |
∵杠杆的长度OB是确定的,只有一个,所以该方程只能取一个解,
∴该方程根的判别式b2-4ac等于0,因为当b2-4ac=0时,方程有两个相等的实数根,即有一个解,
即:则F2-4×
| 1 |
| 2 |
则F2=2mMg2a,
得F=
| 2mMa |
(3)将F=
| 2mMa |
| 1 |
| 2 |
解得OB=
|
故选A.
点评:本题是一道跨学科题,需要学生掌握物理的杠杆知识和数学的一元二次方程的相关知识,题中学生容易出错的地方有三个:①对于杠杆重力的确定;②对于阻力及阻力臂的确定;③对于根的判别式的确定.

练习册系列答案
相关题目
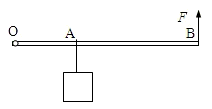 如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?
如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?