题目内容
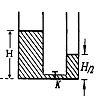
 如图所示,连通器左端试管横截面的半径为2R,右端试管横截面的半径为R.左、右水面的高度分别为H、
如图所示,连通器左端试管横截面的半径为2R,右端试管横截面的半径为R.左、右水面的高度分别为H、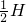 .那么打开开关K后,右管水面能够上升到距离底部的最大高度为
.那么打开开关K后,右管水面能够上升到距离底部的最大高度为
- A.1.5H
- B.1.3H
- C.1.1H
- D.0.9H
B
分析:本题主要考查对连通器构造特点的了解:上端开口,底部连通的仪器叫连通器.
当打开开关K时,左右容器构成一个连通器,根据连通器内液体静止时,液面相平求出此时液面的高度,再根据根据机械能守恒及单摆的原理性进行分析.
解答:当打开开关K时,左右容器构成一个连通器;由于连通器内液体静止时,液面相平,因此左边液体将下降,右面液体将升高,左右容器对容器底部产生的压强相等,并且左边减少水的体积等于右边增加水的体积;设左边液体下降高度为x,
即π(2R)2x=πR2( H-x)
H-x)
4x= H-x
H-x
x=0.1H
因此水面静止时,水面的高度为0.9H,根据机械能守恒及单摆的原理,液面继续上升0.4H,然后开始下降,下降后又上升,一次比一次低,最后静止.
所以达到最大高度0.9H+0.4H=1.3H.
故选B.
点评:本题的解题关键有两个:(1)只有同种液体静止在连通器中,各部分直接与大气接触的液面才总是在同一水平面上.(2)减少水的体积等于增加水的体积.
分析:本题主要考查对连通器构造特点的了解:上端开口,底部连通的仪器叫连通器.
当打开开关K时,左右容器构成一个连通器,根据连通器内液体静止时,液面相平求出此时液面的高度,再根据根据机械能守恒及单摆的原理性进行分析.
解答:当打开开关K时,左右容器构成一个连通器;由于连通器内液体静止时,液面相平,因此左边液体将下降,右面液体将升高,左右容器对容器底部产生的压强相等,并且左边减少水的体积等于右边增加水的体积;设左边液体下降高度为x,
即π(2R)2x=πR2(
 H-x)
H-x)4x=
 H-x
H-xx=0.1H
因此水面静止时,水面的高度为0.9H,根据机械能守恒及单摆的原理,液面继续上升0.4H,然后开始下降,下降后又上升,一次比一次低,最后静止.
所以达到最大高度0.9H+0.4H=1.3H.
故选B.
点评:本题的解题关键有两个:(1)只有同种液体静止在连通器中,各部分直接与大气接触的液面才总是在同一水平面上.(2)减少水的体积等于增加水的体积.

练习册系列答案
相关题目

 如图所示,连通器左端试管横截面的半径为2R,右端试管横截面的半径为R.左、右水面的高度分别为H、
如图所示,连通器左端试管横截面的半径为2R,右端试管横截面的半径为R.左、右水面的高度分别为H、 .那么打开开关K后,右管水面能够上升到距离底部的最大高度为( )
.那么打开开关K后,右管水面能够上升到距离底部的最大高度为( )