题目内容
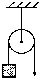
如图所示，利用定滑轮提升一个重为500N的物体，如物体上升0.6m的过程中人的拉力做的功是360J，则此人的拉力是600
600
N，他做的额外功是60
60
J，此定滑轮的机械效率是83.3%
83.3%
．分析：定滑轮中，绳端移动的距离和物体上升的距离相等，根据W=Fs求出此人的拉力；再根据W=Gh求出有用功，总功减去有用功即为额外功，最后根据η=
×100%求出机械效率．
| W有 |
| W总 |
解答：已知：G=500N，h=0.6m，W总=360J
求：（1）拉力F，（2）他做的额外功W额，（3）此定滑轮的机械效率η
解：（1）定滑轮中，绳端移动的距离和物体上升的距离相等，即s=h=0.6m，
根据W=Fs可得：
拉力F=
=
=600N；
（2）他做的有用功：
W有用=Gh=500N×0.6m=300J，
他做的额外功：
W额=W总-W有=360J-300J=60J；
（3）此定滑轮的机械效率：
η=
×100%=
×100%≈83.3%．
故答案为：600；60；83.3%．
求：（1）拉力F，（2）他做的额外功W额，（3）此定滑轮的机械效率η
解：（1）定滑轮中，绳端移动的距离和物体上升的距离相等，即s=h=0.6m，
根据W=Fs可得：
拉力F=
| W总 |
| s |
| 360J |
| 0.6m |
（2）他做的有用功：
W有用=Gh=500N×0.6m=300J，
他做的额外功：
W额=W总-W有=360J-300J=60J；
（3）此定滑轮的机械效率：
η=
| W有 |
| W总 |
| 300J |
| 360J |
故答案为：600；60；83.3%．
点评：本题考查了拉力、额外功和机械效率的计算，关键是明确有用功、额外功、总功之间的关系和知道定滑轮中绳端移动的距离和物体上升的距离相等．
练习册系列答案
相关题目
如图所示，利用定滑轮，动滑轮及滑轮组匀速向上提升重物．已知作用在绳子自由端的拉力F甲=F乙=F丙=50N．则：不计动滑轮重和绳与滑轮之间摩擦时，提升的物重分别是：G甲为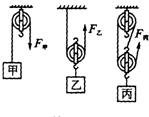
如图所示，利用定滑轮、动滑轮及滑轮组匀速向上提升重物．已知作用在绳子自由端的拉力F甲=F乙=F丙=50 N，则（不计动滑轮重和绳与滑轮之间摩擦），提升的物重分别是：G甲=
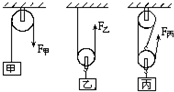如图所示，利用定滑轮、动滑轮及滑轮组匀速向上提升重物．已知作用在绳子自由端的拉力F甲=F乙=F丙=50N．若不计动滑轮重、绳重和摩擦时，提升的物重分别是：G甲为