题目内容
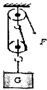 用如图所示滑轮组提升重物.人用300N的拉力F,15s内使重为500N的物体匀速上升了3m.不计绳重和摩擦,求:
用如图所示滑轮组提升重物.人用300N的拉力F,15s内使重为500N的物体匀速上升了3m.不计绳重和摩擦,求:
(1)拉力F做功的功率;
(2)滑轮组的机械效率;
(3)若改提900N的物体,求此时的机械效率.
解:(1)由图知,n=2,s=2h=2×3m=6m,
W总=Fs=300N×6m=1800J;
P=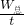 =
=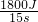 =120W;
=120W;
(2)W有用=Gh=500N×3m=1500J;
η=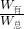 =
= ≈83.3%;
≈83.3%;
(3)∵不计绳重和摩擦,
∴F= (G轮+G物),即:300N=
(G轮+G物),即:300N= (G轮+500N),
(G轮+500N),
∴G轮=100N,
改提900N的物体,
F′= (100N+900N)=500N,
(100N+900N)=500N,
此时的机械效率:
η′= =
=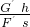 =
=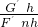 =
= =
=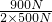 =90%.
=90%.
答:(1)拉力的功率是120W;
(2)滑轮组机械效率约是83.3%;
(3)若提升900N重物,滑轮组机械效率为90%.
分析:(1)知道拉力大小,由滑轮组结构得出承担物重的绳子股数n=2,则s=2h,利用W总=Fs求拉力做功,再利用P= 求拉力做功功率;
求拉力做功功率;
(2)知道物重G和提升的高度,利用W=Gh求有用功;再利用效率公式η=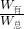 求出滑轮组的机械效率;
求出滑轮组的机械效率;
(3)不计绳重和摩擦,利用F= (G轮+G物)求动滑轮重;改提900N的物体,利用F′=
(G轮+G物)求动滑轮重;改提900N的物体,利用F′= (G轮+G物′)求此时的拉力,再利用η=
(G轮+G物′)求此时的拉力,再利用η=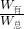 =
= =
=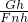 =
=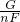 求此时的机械效率.
求此时的机械效率.
点评:本题考查了有用功、总功、功率、机械效率的计算,两次利用好“不计绳重和摩擦,F= (G轮+G物)”是本题的关键.
(G轮+G物)”是本题的关键.
W总=Fs=300N×6m=1800J;
P=
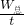 =
=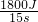 =120W;
=120W;(2)W有用=Gh=500N×3m=1500J;
η=
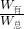 =
= ≈83.3%;
≈83.3%;(3)∵不计绳重和摩擦,
∴F=
 (G轮+G物),即:300N=
(G轮+G物),即:300N= (G轮+500N),
(G轮+500N),∴G轮=100N,
改提900N的物体,
F′=
 (100N+900N)=500N,
(100N+900N)=500N,此时的机械效率:
η′=
 =
=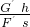 =
=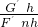 =
= =
=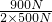 =90%.
=90%.答:(1)拉力的功率是120W;
(2)滑轮组机械效率约是83.3%;
(3)若提升900N重物,滑轮组机械效率为90%.
分析:(1)知道拉力大小,由滑轮组结构得出承担物重的绳子股数n=2,则s=2h,利用W总=Fs求拉力做功,再利用P=
 求拉力做功功率;
求拉力做功功率;(2)知道物重G和提升的高度,利用W=Gh求有用功;再利用效率公式η=
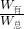 求出滑轮组的机械效率;
求出滑轮组的机械效率;(3)不计绳重和摩擦,利用F=
 (G轮+G物)求动滑轮重;改提900N的物体,利用F′=
(G轮+G物)求动滑轮重;改提900N的物体,利用F′= (G轮+G物′)求此时的拉力,再利用η=
(G轮+G物′)求此时的拉力,再利用η=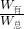 =
= =
=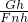 =
=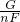 求此时的机械效率.
求此时的机械效率.点评:本题考查了有用功、总功、功率、机械效率的计算,两次利用好“不计绳重和摩擦,F=
 (G轮+G物)”是本题的关键.
(G轮+G物)”是本题的关键. 
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 用如图所示滑轮组提升重物.人用250N的拉力F,10s内使重为400N的物体匀速上升了2m.不计绳重和摩擦,求:
用如图所示滑轮组提升重物.人用250N的拉力F,10s内使重为400N的物体匀速上升了2m.不计绳重和摩擦,求: (2005?茂名)用如图所示滑轮组提升重物时,画出最省力的绳子绕法.
(2005?茂名)用如图所示滑轮组提升重物时,画出最省力的绳子绕法. 某工人用如图所示滑轮组提升重物,工人用250N拉力将重为400N的重物匀速提升10m,请根据提供的信息,计算三个相关的物理量.
某工人用如图所示滑轮组提升重物,工人用250N拉力将重为400N的重物匀速提升10m,请根据提供的信息,计算三个相关的物理量. 用如图所示滑轮组提升重物.人用50N的拉力F,15s内使重为90N的物体匀速上升了3m.不计绳重和摩擦,求:
用如图所示滑轮组提升重物.人用50N的拉力F,15s内使重为90N的物体匀速上升了3m.不计绳重和摩擦,求: 用如图所示滑轮组提升重物,已知物体重300N,作用在绳端的拉力为125N,物体在拉力作用下以0.5m/s的速度匀速上升,不计绳重和摩擦,试求:
用如图所示滑轮组提升重物,已知物体重300N,作用在绳端的拉力为125N,物体在拉力作用下以0.5m/s的速度匀速上升,不计绳重和摩擦,试求: