题目内容
一根长40厘米粗细均匀的杠杆(不计杠杆的重力),左端挂20克钩码,右端挂30克钩码当杠杆平衡时,支点应距左端 厘米处;如果将支点向右移6厘米,同时左端的钩码数不变,要使杠杆重新平衡,右端应加挂 克钩码.
【答案】分析:①两钩码施加竖直向下的重力,故力臂为支点到悬点的距离,因杠杆为水平平衡则两力臂之和为杆长,知道两端钩码的质量,可利用公式G=mg计算出钩码的重力,利用杠杆的平衡条件计算出支点应距左端的距离.
②将支点向右移6厘米,可以求出两边力臂的大小,又知道左边所挂钩码的重,利用杠杆的平衡条件求右边应挂钩码的重,再利用公式m=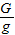 计算出钩码的质量.
计算出钩码的质量.
解答:解:①杠杆的长为40cm=0.4m,
而G左=m左g=0.02kg×10N/kg=0.2N,G右=m右g=0.03kg×10N/kg=0.3N,
设支点离左端为L,则左端力臂为L,右端力臂为(0.4m-L),
由杠杆的平衡条件得:G左L=G右(0.4m-L),
即:0.2N×L=0.3N×(0.4m-L),
解得:L=0.24m=24cm.
②∵将支点向右移6厘米,
∴左端的力臂为:L左=24cm+6cm=30cm=0.3m,L右=L-L左=0.4m-0.3m=0.1m,
而左端的钩码数不变,仍为G左=0.2N,
由杠杆的平衡条件得:G左L左=G右′L右,
即0.2N×0.3m=G右′×0.1m,
解得:G右′=0.6N,
∴右端钩码的质量为:m右′=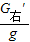 =
=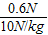 =0.06kg=60g.
=0.06kg=60g.
故答案为;24;60.
点评:本题考查了学生对杠杆的平衡条件的掌握和运用,会根据杠杆平衡的条件计算力臂的长度,会根据杠杆平衡的条件计算出物体的重力.
②将支点向右移6厘米,可以求出两边力臂的大小,又知道左边所挂钩码的重,利用杠杆的平衡条件求右边应挂钩码的重,再利用公式m=
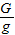 计算出钩码的质量.
计算出钩码的质量.解答:解:①杠杆的长为40cm=0.4m,
而G左=m左g=0.02kg×10N/kg=0.2N,G右=m右g=0.03kg×10N/kg=0.3N,
设支点离左端为L,则左端力臂为L,右端力臂为(0.4m-L),
由杠杆的平衡条件得:G左L=G右(0.4m-L),
即:0.2N×L=0.3N×(0.4m-L),
解得:L=0.24m=24cm.
②∵将支点向右移6厘米,
∴左端的力臂为:L左=24cm+6cm=30cm=0.3m,L右=L-L左=0.4m-0.3m=0.1m,
而左端的钩码数不变,仍为G左=0.2N,
由杠杆的平衡条件得:G左L左=G右′L右,
即0.2N×0.3m=G右′×0.1m,
解得:G右′=0.6N,
∴右端钩码的质量为:m右′=
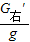 =
=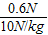 =0.06kg=60g.
=0.06kg=60g.故答案为;24;60.
点评:本题考查了学生对杠杆的平衡条件的掌握和运用,会根据杠杆平衡的条件计算力臂的长度,会根据杠杆平衡的条件计算出物体的重力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目