题目内容
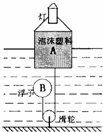 科技小组的同学用长方体泡沫塑料A、三脚架和灯泡等制作了一个航标灯模型(如图),总重为4N,A 底部与浮子B 用细绳相连.水位上升时,浮子B 下降;水位下降时,浮子B 上升,使航标灯静止时A 浸人水中的深度始终为5cm,排开水的质量为500g,浮子B 重0.5N (不计绳重和绳与滑轮间的摩擦,g=10N/kg)
科技小组的同学用长方体泡沫塑料A、三脚架和灯泡等制作了一个航标灯模型(如图),总重为4N,A 底部与浮子B 用细绳相连.水位上升时,浮子B 下降;水位下降时,浮子B 上升,使航标灯静止时A 浸人水中的深度始终为5cm,排开水的质量为500g,浮子B 重0.5N (不计绳重和绳与滑轮间的摩擦,g=10N/kg)求:(1)泡沫塑料A 底部受到水的压强是多少?
(2)航标灯静止时,浮子B 体积应为多大?
(3)浮子B的平均密度是多少.
分析:(1)知道泡沫塑料A底部所处的深度和水的密度,利用液体压强公式求其受到的压强大小;
(2)知道航标灯静止时排开水的质量,利用阿基米德原理求航标灯受到的浮力;然后对沫塑料A受力分析可知,泡沫塑料A的拉力等于泡沫塑料A受到的浮力减去航标灯模型的总重;航标灯静止时,浮子B受的浮力(竖直向上)等于竖直向下的重力加上拉力,而再利用阿基米德原理求浮子B的体积;
(3)已知浮子的重,根据G=mg求出其质量,再根据密度公式求出浮子B的平均密度.
(2)知道航标灯静止时排开水的质量,利用阿基米德原理求航标灯受到的浮力;然后对沫塑料A受力分析可知,泡沫塑料A的拉力等于泡沫塑料A受到的浮力减去航标灯模型的总重;航标灯静止时,浮子B受的浮力(竖直向上)等于竖直向下的重力加上拉力,而再利用阿基米德原理求浮子B的体积;
(3)已知浮子的重,根据G=mg求出其质量,再根据密度公式求出浮子B的平均密度.
解答:解:(1)A底部受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×0.05m=500Pa;
(2)航标灯静止时:
F浮A=G排=0.5kg×10N/kg=5N;
A受到的绳子的拉力:
FA=F浮A-G=5N-4N=1N;
绳子对B向下的拉力:
FB=FA=1N,
浮子B受到的浮力:
F浮=GB+FB=0.5N+1N=1.5N
浮子B的体积为:
V=V排=
=
=1.5×10-4m3.
(3)浮子B的平均密度:
ρ=
=
=
≈0.33×103kg/m3.
答:(1)泡沫塑料A底部受到水的压强是500Pa;
(2)航标灯静止时,浮子B体积应为1.5×10-4m3;
(3)浮子B的平均密度约为0.33×103kg/m3.
p=ρgh=1×103kg/m3×10N/kg×0.05m=500Pa;
(2)航标灯静止时:
F浮A=G排=0.5kg×10N/kg=5N;
A受到的绳子的拉力:
FA=F浮A-G=5N-4N=1N;
绳子对B向下的拉力:
FB=FA=1N,
浮子B受到的浮力:
F浮=GB+FB=0.5N+1N=1.5N
浮子B的体积为:
V=V排=
| F浮 |
| ρ水g |
| 1.5N |
| 1.0×103kg/m3×10N/kg |
(3)浮子B的平均密度:
ρ=
| m |
| V |
| G |
| Vg |
| 0.5N |
| 1.5×10-4m3×10N/kg |
答:(1)泡沫塑料A底部受到水的压强是500Pa;
(2)航标灯静止时,浮子B体积应为1.5×10-4m3;
(3)浮子B的平均密度约为0.33×103kg/m3.
点评:本题考查了力的合成(力的平衡)、阿基米德原理、物体的浮沉条件(漂浮条件)、密度公式、液体的压强计算,正确对浮子B进行受力分析是本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
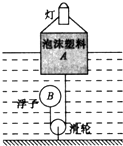 科技小组的同学用长方体泡沫塑料A、三脚架和灯泡等制作了一个航标灯模型(如图),总重为4N,A底部与浮子B用细绳相连.水位上升时,浮子B下降;水位下降时,浮子B上升,使航标灯静止时A浸入水中的深度始终为5cm,排开水的质量为500g,浮子B重为0.5N(不计绳重和绳与滑轮间的摩擦)
科技小组的同学用长方体泡沫塑料A、三脚架和灯泡等制作了一个航标灯模型(如图),总重为4N,A底部与浮子B用细绳相连.水位上升时,浮子B下降;水位下降时,浮子B上升,使航标灯静止时A浸入水中的深度始终为5cm,排开水的质量为500g,浮子B重为0.5N(不计绳重和绳与滑轮间的摩擦)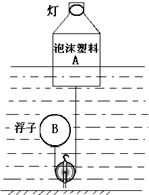 (2009?昌平区二模)如图所示,科技小组的同学用长方体泡沫塑料、三脚架和灯泡等制作了一个航标灯模型A,A部分总重为4N,A底部与浮子B用细绳相连.某时刻航标灯静止时,长方体泡沫塑料浸入水中的深度为5cm,排开水的质量为500g,浮子B重 0.5N(不计绳重和绳与滑轮间的摩擦,g取10N/kg),则下列选项正确的是( )
(2009?昌平区二模)如图所示,科技小组的同学用长方体泡沫塑料、三脚架和灯泡等制作了一个航标灯模型A,A部分总重为4N,A底部与浮子B用细绳相连.某时刻航标灯静止时,长方体泡沫塑料浸入水中的深度为5cm,排开水的质量为500g,浮子B重 0.5N(不计绳重和绳与滑轮间的摩擦,g取10N/kg),则下列选项正确的是( )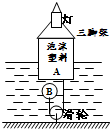 科技小组的同学用长方体泡沫塑料A、三脚架和灯泡等制作了一个航标灯模型如图所示.模型总质量为mA,底面积为SA,A底部与浮子B 通过滑轮用细绳相连.水位上升时,浮子B下降;水位下降时,浮子B上升,保持航标灯静止时A浸入水中的深度始终为h,浮子B质量为mB,则浮子B的体积为
科技小组的同学用长方体泡沫塑料A、三脚架和灯泡等制作了一个航标灯模型如图所示.模型总质量为mA,底面积为SA,A底部与浮子B 通过滑轮用细绳相连.水位上升时,浮子B下降;水位下降时,浮子B上升,保持航标灯静止时A浸入水中的深度始终为h,浮子B质量为mB,则浮子B的体积为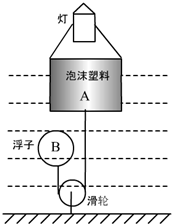 重庆一中航模科技小组的同学用长方体塑料A、小铝丝和LED小电筒等制作了一个高为25cm航标指示灯模型,如图所示,航标指示灯模型重为6N. A 底部用细绳与浮子B(始终浸没在水中)相连,浮子B 重1N.若水位上升时,浮子B 可下降;若水位下降时,浮子B可上升;使航标灯静止时A竖直且水面以下的高度始终为10cm,排开水的质量为1000g.当航标灯静止时(不计绳重和绳与滑轮间的摩擦),求:
重庆一中航模科技小组的同学用长方体塑料A、小铝丝和LED小电筒等制作了一个高为25cm航标指示灯模型,如图所示,航标指示灯模型重为6N. A 底部用细绳与浮子B(始终浸没在水中)相连,浮子B 重1N.若水位上升时,浮子B 可下降;若水位下降时,浮子B可上升;使航标灯静止时A竖直且水面以下的高度始终为10cm,排开水的质量为1000g.当航标灯静止时(不计绳重和绳与滑轮间的摩擦),求: