题目内容
【题目】如图,电源电压恒为12V,定值电阻R1=20Ω。

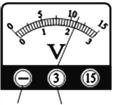
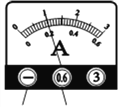
(1)当开关S、S1闭合,S2断开,滑动变阻器R的滑片移到它的中点位置时,电流表的示数为0.3A,求:滑动变阻器的最大阻值;
(2)当开关S、S1、S2闭合,滑动变阻器的滑片移到a端时,电流表的示数变为0.8A,求:定值电阻R2的阻值;
(3)求此电路消耗的最小总电功率
【答案】(1)40Ω (2) 60Ω (3)1.44W
【解析】(1)当开关S、S1闭合,S2断开,滑动变阻器R的滑片移到它的中点位置时,R1 与R的最大阻值的一半串联,电流表测电路中的电流,由I=U/R可得,电路中的总电阻R总 =U/I=12V/0.3A=40Ω,因串联电路中总电阻等于各分电阻之和,所以,滑动变阻器的最大阻值: R=2(R总 -R1) =2(40Ω-20Ω)=40Ω;
(2)当开关S、S1、S2闭合,滑动变阻器的滑片移到a端时,R1与R2并联,电流表测电路中的电流,由I=U/R可得,电路中的总电阻R总并= U/I=12V/0.8A=15Ω;因并联电路中总电阻的倒数等于各分电阻倒数之和,即电路中的总电阻:
R总 =R1R2/R1+R2,所以R2=60Ω;
(3)根据题意当滑动变阻器的最大值与R2串联时,回路的电阻最大,电路的功率最小,最小功率P=UI小=12V×12V/(40+60)Ω=1.44W。

练习册系列答案
相关题目