��Ŀ����
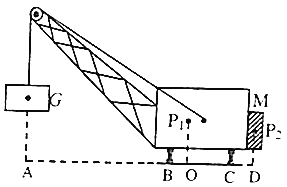
����Ŀ����ͼ��ʾ��һ�����ػ���ʾ��ͼ�����ػ���2.4��104N���������ۣ�������ΪP1��Ϊʹ���ػ��������ʱ�����㵹�������Ҳ�������M������ΪP2�����ֲ��ABΪ10m��BOΪ1m��BCΪ4m��CDΪ1.5m����gȡ10N/kg��
��1���������ػ����������6m����ʱ5Os��������������ƽ���ٶ��Ƕ��٣�
��2������ˮƽ����������Ϊ2.44��104N�Ļ��䣬�������ĽӴ������3m2��
�������ػ��������أ����������ʱ������ʹ����Ե����ѹǿ���ٶ��٣�
����Ҫ����˻��䣬���ػ�������Ӷ���ţ�����أ�
��3��������Ϊ���ػ�������Խ��Խ�ã��������ܵ�����ص���������ػ�����8t����������˵�����ɣ�
���𰸡���1��0.12m/s����2��������800Pa�����������4��104N�����أ�
��3�������ػ�������8t�����أ��������ػ��ڲ�����ʱ�����ҷ�����
��������
�����������1������������ƽ���ٶȣ�![]() ��
��
��2�����������ɾ�ֹ�ڵ�����ʱ���Ե����ѹǿ��![]() �������ػ��������أ����������ʱ��֧��ΪB���Ի��������F�������ݸܸ�ƽ�������У�F����AB=G���ػ���BO��
�������ػ��������أ����������ʱ��֧��ΪB���Ի��������F�������ݸܸ�ƽ�������У�F����AB=G���ػ���BO��
����F����10m=2.4��104N��1m����ã�F��=2400N��
��ʱ����Ե����ѹ����F2=G������F��=2.44��104N��2400N=2.2��104N��
��ʱ����Ե����ѹǿ��![]() ��
��
����ѹǿ�仯����![]() ��
��
����Ҫ����˻��䣬���ػ��Ի����������F����=G=2.44��104N��
֧��ΪB�����ص����ۣ�BD=BC+CD=4m+1.5m=5.5m��
���ݸܸ�ƽ�������ɵã�F�����AB=G���ػ���BO+G������BD������2.44��104N��10m=2.4��104N��1m+G������5.5m��
��ã�G����=4��104N��
��3�����������ʱ��֧��ΪC�����ػ����ص����ۣ�OC=BC��BO=4m��1m=3m�����ص����ۣ�CD=1.5m��
���ݸܸ�ƽ�������ɵã�G���ػ���OC=G�������CD������2.4��104N��3m=G�������1.5m��
���������أ�G������=4.8��104N��������ص�������![]() ��
��
��Ϊ4.8t��8t�����������ػ�������8t�����أ��������ػ��ڲ�����ʱ�����ҷ�����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��
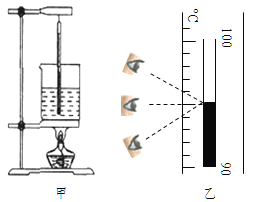
��1����ͼ����ʾ���¶ȵ���ȷ������ ________ ��C��
��2����ˮ����ʱ��ˮ����һ�����ݴ�Aλ�ã����ΪVA��������Bλ�ã����ΪVB������VA_______VB��ѡ����>������=������<������ͬ����������A��B��λ���ܵ�ˮ��ѹǿ�ֱ�ΪpA��pB����pA______ pB��
ʱ��/min | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
�¶�/��C | 90 | 92 | 94 | 96 | 98 | 98 | 98 | 98 | 98 |
��3�����ϱ����е�������С����¼��ʵ�����ݣ���ˮ�ķе��� _______ ��C��
��4��ʵ����ɺ��ձ���ˮ��������ʵ��ǰ��� ________��ѡ�������������������������С������

