题目内容
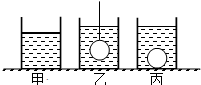 (2013?丰台区一模)盛有液体的圆柱形容器置于水平桌面上,如图甲所示,容器对桌面的压力为N1,容器对桌面的压强为p1;用细线拴一金属球,将金属球浸没在液体中,如图乙所示,容器对桌面的压强为p2;将细线剪断,金属球沉到容器底部,如图丙所示,金属球对容器底部的压力为N3.p1:p2=5:6,N1:N3=5:9,液体的密度是0.9g/cm3,g取10N/kg.则金属球的密度为
(2013?丰台区一模)盛有液体的圆柱形容器置于水平桌面上,如图甲所示,容器对桌面的压力为N1,容器对桌面的压强为p1;用细线拴一金属球,将金属球浸没在液体中,如图乙所示,容器对桌面的压强为p2;将细线剪断,金属球沉到容器底部,如图丙所示,金属球对容器底部的压力为N3.p1:p2=5:6,N1:N3=5:9,液体的密度是0.9g/cm3,g取10N/kg.则金属球的密度为9
9
g/cm3.分析:设乙图中容器对桌面的压力为N2,根据水平面上物体的压力和自身的重力相等表示出甲乙两图容器对桌面的压强,利用受力面积不变可求两者的压力之比,图乙中对桌面增大的压力等于小球排开液体的重力,根据阿基米德原理可知增加的重力等于金属球受到的浮力,进一步求出N1与金属球受到浮力的比值,图丙中金属球对容器底部的压力等于金属球的重力减去受到的浮力,进一步求出金属球受到浮力和自身重力之间的关系,最后根据重力公式、密度公式、阿基米德原理求出金属球密度和液体密度之间的关系即可求出金属球的密度.
解答:解:设N2为乙图中容器对桌面的压力,
∵p=
,
∴
=
=
=
,
∵如乙中桌面受到增加的压力等于小球排开液体的重力,即小球受到的浮力,
∴
=
=
,
解得:N1=5F浮,
=
,
图丙中,金属球对容器底部的压力等于自身的重力减去受到的浮力,
∴
=
=
,
解得:
=
,
∵G=mg,ρ=
,F浮=ρgV排,V排=V
∴
=
=
=
=
,
解得:ρ=10ρ液=10×0.9g/cm3=9g/cm3.
故答案为:9.
∵p=
| F |
| S |
∴
| p1 |
| p2 |
| ||
|
| N1 |
| N2 |
| 5 |
| 6 |
∵如乙中桌面受到增加的压力等于小球排开液体的重力,即小球受到的浮力,
∴
| N1 |
| N2 |
| N1 |
| N1+F浮 |
| 5 |
| 6 |
解得:N1=5F浮,
| F浮 |
| N1 |
| 1 |
| 5 |
图丙中,金属球对容器底部的压力等于自身的重力减去受到的浮力,
∴
| N1 |
| N3 |
| 5F浮 |
| G-F浮 |
| 5 |
| 9 |
解得:
| G |
| F浮 |
| 10 |
| 1 |
∵G=mg,ρ=
| m |
| V |
∴
| G |
| F浮 |
| mg |
| ρ液gV |
| ρVg |
| ρ液gV |
| ρ |
| ρ液 |
| 10 |
| 1 |
解得:ρ=10ρ液=10×0.9g/cm3=9g/cm3.
故答案为:9.
点评:本题考查了金属球密度的计算,涉及到压强公式、重力公式、力平衡条件的应用,关键是利用三图各量之间的关系得出金属球重力和受到浮力之间的关系.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目