题目内容
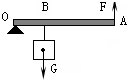 某工地在冬季水利建设中设计了一个提起重物的机械,如图所示是这个机械一个组成部分的示意图.OA是根钢管,每米受重力为30N;O是转动轴;重物的质量m为150kg,挂在B处,OB=1m;拉力F加在A点,竖直向上,取g=10N/kg.为维持钢管水平平衡,OA为
某工地在冬季水利建设中设计了一个提起重物的机械,如图所示是这个机械一个组成部分的示意图.OA是根钢管,每米受重力为30N;O是转动轴;重物的质量m为150kg,挂在B处,OB=1m;拉力F加在A点,竖直向上,取g=10N/kg.为维持钢管水平平衡,OA为10
10
m时所用的拉力最小.分析:应用杠杆平衡条件F1L1=F2L2分析答题:本题中动力为F,动力臂为OA,而阻力有两个(一个是重物G,另一个是钢管本身的重力),所以阻力臂也有两个(重物G的力臂是OB,钢管重力的力臂是
OA),明确了动力、动力臂、阻力和阻力臂之后,根据杠杆平衡条件列出一个方程,然后应用数学知识分析答题.
| 1 |
| 2 |
解答:解:由题意可知,杠杆的动力为F,动力臂为OA,
阻力分别是重物G物和钢管的重力G钢管,阻力臂分别是OB和
OA,
重物的重力G物=m物g=150kg×10N/kg=1500N,
钢管的重力G钢管=30N×OA,
由杠杆平衡条件得:F?OA=G物?OB+G钢管?
OA,
即F?OA=1500N×1m+30N?OA?
OA,
得:F?OA=1500+15?OA2,
移项得:15?OA2-F?OA+1500=0,
由于钢管的长度OA是确定的只有一个,所以该方程只能取一个解,
因为当b2-4ac=0时,方程有两个相等的实数根,即有一个解,因此应该让根的判别式b2-4ac等于0,
即F2-4×15×1500=0,F2-90000=0,解得:F=300N,
将F=300N代入方程15?OA2-F?OA+1500=0,解得OA=10m.
故答案为:10.
阻力分别是重物G物和钢管的重力G钢管,阻力臂分别是OB和
| 1 |
| 2 |
重物的重力G物=m物g=150kg×10N/kg=1500N,
钢管的重力G钢管=30N×OA,
由杠杆平衡条件得:F?OA=G物?OB+G钢管?
| 1 |
| 2 |
即F?OA=1500N×1m+30N?OA?
| 1 |
| 2 |
得:F?OA=1500+15?OA2,
移项得:15?OA2-F?OA+1500=0,
由于钢管的长度OA是确定的只有一个,所以该方程只能取一个解,
因为当b2-4ac=0时,方程有两个相等的实数根,即有一个解,因此应该让根的判别式b2-4ac等于0,
即F2-4×15×1500=0,F2-90000=0,解得:F=300N,
将F=300N代入方程15?OA2-F?OA+1500=0,解得OA=10m.
故答案为:10.
点评:本题是一道跨学科题,解答此题不仅涉及到物理知识,还应用到数学方面的知识.
本题的难点:①对于钢管重力的确定;②对于阻力及阻力臂的确定;③对于根的判别式的确定.
本题的难点:①对于钢管重力的确定;②对于阻力及阻力臂的确定;③对于根的判别式的确定.

练习册系列答案
相关题目
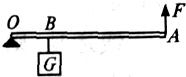 某工地在冬季水利建设中设计了一个提起重物的机械,其中的一部分结构如图所示、OA是一个均匀直管,不计直管质量,O是转动轴;重物的质量m为150 kg,挂在B处,OA=3 m,OB=1 m;拉力F方向始终向上,为维持平衡,拉力F作用在直管上哪点时,且直管如何放置,才能使力F最小,最小力为多少?
某工地在冬季水利建设中设计了一个提起重物的机械,其中的一部分结构如图所示、OA是一个均匀直管,不计直管质量,O是转动轴;重物的质量m为150 kg,挂在B处,OA=3 m,OB=1 m;拉力F方向始终向上,为维持平衡,拉力F作用在直管上哪点时,且直管如何放置,才能使力F最小,最小力为多少?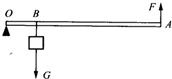 (2003?安徽)某工地在冬季水利建设中设计了一个提起重物的机械,其中的一部分结构如图所示.OA是一个均匀钢管,每米长所受重力为30N;O是转动轴;重物的质量m为150kg,挂在B处,OB=1m;拉力F作用在A点,竖直向上.为维持平衡,钢管OA为多长时所用的拉力最小?这个最小拉力是多少?(g取10N/kg)
(2003?安徽)某工地在冬季水利建设中设计了一个提起重物的机械,其中的一部分结构如图所示.OA是一个均匀钢管,每米长所受重力为30N;O是转动轴;重物的质量m为150kg,挂在B处,OB=1m;拉力F作用在A点,竖直向上.为维持平衡,钢管OA为多长时所用的拉力最小?这个最小拉力是多少?(g取10N/kg)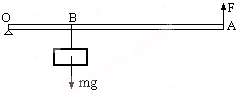 某工地在冬季水利建设中设计了一个提起重物的机械,如图是这个机械一个组成部分的示意图.OA是个钢管,每米长受重力为30牛顿;0是转动轴;重物的质量m为150千克,挂在B处,0B=1米;拉力F加在A点,竖直向上.取g=1 0牛/千克.为维持平衡,钢管OA为多长时所用的拉力最小?这个最小拉力是多少?
某工地在冬季水利建设中设计了一个提起重物的机械,如图是这个机械一个组成部分的示意图.OA是个钢管,每米长受重力为30牛顿;0是转动轴;重物的质量m为150千克,挂在B处,0B=1米;拉力F加在A点,竖直向上.取g=1 0牛/千克.为维持平衡,钢管OA为多长时所用的拉力最小?这个最小拉力是多少?