题目内容
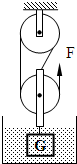 (2008?房山区一模)重480N的物体浸没在底面积为4000cm2的柱形盛水容器中,用滑轮组将它提升,如图所示.物体上升10cm所用的时间为2s,拉力的功率为20W,此时物体仍在水面以下.当物体离开水面时,水对容器底的压强减少了500Pa(不计绳重及轮与轴之间的摩擦,取g=10N/kg),求:物体出水前后,滑轮组的机械效率之比.
(2008?房山区一模)重480N的物体浸没在底面积为4000cm2的柱形盛水容器中,用滑轮组将它提升,如图所示.物体上升10cm所用的时间为2s,拉力的功率为20W,此时物体仍在水面以下.当物体离开水面时,水对容器底的压强减少了500Pa(不计绳重及轮与轴之间的摩擦,取g=10N/kg),求:物体出水前后,滑轮组的机械效率之比.分析:由图知,滑轮组承担物重的绳子股数n=3,则s=3h.
物体在水中时,知道物体上升的高度和时间,利用速度公式可求物体上升速度,则拉力端移动的速度为物体上升速度的3倍,知道拉力做功功率,利用P=Fv求拉力大小;
知道当物体离开水面时,水对容器底的压强减少值,利用压强公式求减小的压力值(浮力大小),滑轮组对物体的拉力等于物体重减去浮力,根据效率公式η=
求物体在水中滑轮组的机械效率;
不计绳重及轮与轴之间的摩擦,利用F=
(F拉+G动)求动滑轮重,再利用η=
求物体出水后的滑轮组的机械效率,进而求出物体出水前后,滑轮组的机械效率之比.
物体在水中时,知道物体上升的高度和时间,利用速度公式可求物体上升速度,则拉力端移动的速度为物体上升速度的3倍,知道拉力做功功率,利用P=Fv求拉力大小;
知道当物体离开水面时,水对容器底的压强减少值,利用压强公式求减小的压力值(浮力大小),滑轮组对物体的拉力等于物体重减去浮力,根据效率公式η=
| F拉 |
| nF |
不计绳重及轮与轴之间的摩擦,利用F=
| 1 |
| n |
| G |
| G+G动 |
解答:解:
物体在水中时:
∵P=Fυ,即:20W=F×
×3,
∴F=
N,
F浮=△PS=500Pa×0.4m2=200N,
F拉=G-F浮=480N-200N=280N,
η前=
=
=70%;
∵不计绳重及轮与轴之间的摩擦,
∴F=
(F拉+G动),
N=
(280N+G动)
∴G动=120N,
物体被拉出水后:
η后=
=
=80%,
=
=
.
答:物体出水前后,滑轮组的机械效率之比7:8.
物体在水中时:
∵P=Fυ,即:20W=F×
| 0.1m |
| 2s |
∴F=
| 400 |
| 3 |
F浮=△PS=500Pa×0.4m2=200N,
F拉=G-F浮=480N-200N=280N,
η前=
| F拉 |
| nF |
| 280N | ||
3×
|
∵不计绳重及轮与轴之间的摩擦,
∴F=
| 1 |
| n |
| 400 |
| 3 |
| 1 |
| 3 |
∴G动=120N,
物体被拉出水后:
η后=
| G |
| G+G动 |
| 480N |
| 480N+120N |
| η前 |
| η后 |
| 70% |
| 80% |
| 7 |
| 8 |
答:物体出水前后,滑轮组的机械效率之比7:8.
点评:本题为力学综合题,考查了压强公式的应用、浮力的计算、同一直线上力的合成、使用滑轮组拉力和机械效率的计算,本题关键是明确物体出水前后机械效率的计算方法,属于难题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
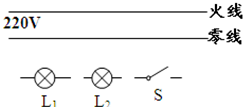 (2008?房山区一模)教室里通常用一只开关同时控制两盏灯,如图所示,把开关S和两盏灯L1、L2正确连入电路中.
(2008?房山区一模)教室里通常用一只开关同时控制两盏灯,如图所示,把开关S和两盏灯L1、L2正确连入电路中.