题目内容
甲、乙两车都做匀速直线运动,甲车在乙车前面20m处,并且比乙车早2s运动,甲车的速度是3m/s,乙车的速度是18km/h,问:
(1)乙车要用多少时间追上甲车?
(2)当乙车追上甲车时,甲车离出发地多远?
解:(1)v乙=18km/h=5m/s,设乙车追上甲车需要的时间为t乙,
∵v= ,
,
∴根据题意得:
s甲+20m=s乙
即:3m/s×(t乙+2s)+20m=5m/s×t乙
解得:t乙=12s;
(2)当乙车追上甲车时,甲车所用的时间为:t甲=12s+2s=14s;
∵v= ,
,
∴甲车离出发地的距离为:s=v甲t甲=3m/s×14s=42m.
答:(1)乙车要用14s追上甲车.
(2)当乙车追上甲车时,甲车离出发地42m.
分析:(1)乙车要追上甲车隐含了两车通过的距离关系(乙车通过的距离比甲通过的距离多20m),根据速度的计算公式列式计算即可;
(2)已知甲车的速度和运行的时间,根据速度公式变形计算.
点评:本题考查速度公式的应用,在计算的过程中,一定要注意分析题目中的隐含条件.
∵v=
 ,
,∴根据题意得:
s甲+20m=s乙
即:3m/s×(t乙+2s)+20m=5m/s×t乙
解得:t乙=12s;
(2)当乙车追上甲车时,甲车所用的时间为:t甲=12s+2s=14s;
∵v=
 ,
,∴甲车离出发地的距离为:s=v甲t甲=3m/s×14s=42m.
答:(1)乙车要用14s追上甲车.
(2)当乙车追上甲车时,甲车离出发地42m.
分析:(1)乙车要追上甲车隐含了两车通过的距离关系(乙车通过的距离比甲通过的距离多20m),根据速度的计算公式列式计算即可;
(2)已知甲车的速度和运行的时间,根据速度公式变形计算.
点评:本题考查速度公式的应用,在计算的过程中,一定要注意分析题目中的隐含条件.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
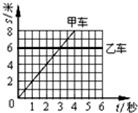 (2011?嘉定区一模)甲、乙两小车运动的s-t图象如图所示,由图象可知( )
(2011?嘉定区一模)甲、乙两小车运动的s-t图象如图所示,由图象可知( ) (2013?虹口区三模)甲乙两小车运动的s-t图象如图所示,由图象可知( )
(2013?虹口区三模)甲乙两小车运动的s-t图象如图所示,由图象可知( )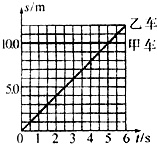 甲、乙两小车运动的s-t图象如图所示,由图象可知( )
甲、乙两小车运动的s-t图象如图所示,由图象可知( )