题目内容
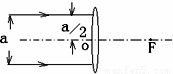
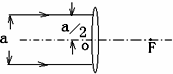如图所示，一束与主光轴平行的光束宽度为a，照射到一个焦距为f的凸透镜上，在凸透镜后面放一个垂直于主轴的光屏，测得在光屏上形成光斑的宽度为b，则光屏到凸透镜的距离为（ ）分析：此题分两种情况，①光斑在经凸透镜折射后，过焦点并继续延长折射光线时得到的，即光斑在焦点右侧．利用相似三角形的对应变成比例求得即可．
②当一束与主光轴平行的光束经凸透镜折射后，还没有汇聚在焦点上时，即在焦点的左侧时，利用相似三角形的对应变成比例求得即可．
②当一束与主光轴平行的光束经凸透镜折射后，还没有汇聚在焦点上时，即在焦点的左侧时，利用相似三角形的对应变成比例求得即可．
解答：解：（1）平行于凸透镜主光轴的光线，经凸透镜折射后过焦点；将图中折射光线延长，与主光轴交与点F，则光屏上形成光斑的宽度为CD即为b，如下图所示：
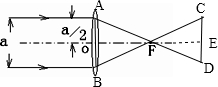
AB=a，CD=b，由△AOF∽△CEF得
=
，即
=
，则FE=
f，
那么光屏到凸透镜的距离为FE+OF=
f+f=（1+
）f．
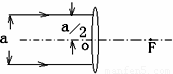
（2）当一束与主光轴平行的光束经凸透镜折射后，还没有汇聚在焦点上时，即在焦点的左侧时，如下图所示：
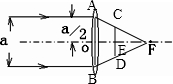
AB=a，CD=b，由△AOF∽△CEF得
=
，即
=
，则FE=
f，
那么光屏到凸透镜的距离为OF-FE=f-
f=（1-
）f．
故选BD．
AB=a，CD=b，由△AOF∽△CEF得
| OF |
| FE |
| AO |
| ED |
| f |
| FE |
| ||
|
| b |
| a |
那么光屏到凸透镜的距离为FE+OF=
| b |
| a |
| b |
| a |
（2）当一束与主光轴平行的光束经凸透镜折射后，还没有汇聚在焦点上时，即在焦点的左侧时，如下图所示：
AB=a，CD=b，由△AOF∽△CEF得
| AO |
| CE |
| OF |
| EF |
| ||
|
| f |
| EF |
| b |
| a |
那么光屏到凸透镜的距离为OF-FE=f-
| b |
| a |
| b |
| a |
故选BD．
点评：本题考查凸透镜对光的作用以及相似三角形对应边成比例的性质，属于一道跨学科的题目，综合性较强而且有一定难度，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一束与主光轴平行的光束宽度为a，照射到一个焦距为f的凸透镜上，在凸透镜后面放一个垂直于主轴的光屏，测得在光屏上形成光斑的宽度为b，则光屏到凸透镜的距离为
