题目内容
如图是某港口卸载货物的简易装置示意图.该装置由悬挂机构、提升装置和行走装置三部分组成.悬挂机构由固定杆OF和杠杆BD构成,O为杠杆DB的支点.配重E通过绳子竖直拉着杠杆D端,行走装置K安装在杠杆DB上,电动机Q可以使其沿BO水平滑动,行走装置和提升电动机及定滑轮的总质量mK是动滑轮质量的2.5倍.当行走装置处于杠杆DB上M点的位置时,提升电动机拉动绳子,通过滑轮组竖直打捞落入水中的货物A.A完全在水中匀速上升的过程中,提升电动机绳子的拉力为F1,滑轮组的机械效率为η1=87.5%,OD:OM=1:2,地板对配重E的支持力为N1;A全部露出水面匀速竖直上升的过程中,提升电动机绳子的拉力为F2,滑轮组的机械效率为η2,当A静止后,电动机Q启动,水平向左拉动行走装置至点C(图中未标出),使物体静止在海岸上方,以方便卸载货物,此时OD:OC=5:2,地板对配重E的支持力为N2.滑轮组提升A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置平衡.已知提升电动机输出功率恒定,A在水中与出水后匀速运动速度v1:v2=5:4,A的体积是配重E的体积的2倍,配重E的金属密度是物体A的密度的6倍,细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg.求:(1)打捞前后提升电动机绳子的拉力F1与F2的比值;
(2)货物A打捞出水后的机械效率η2;
(3)货物A出水前后地板对配重E的支持力N1与N2的比值.

【答案】分析:(1)根据电动机输出功率恒定及A在水中与出水后匀速运动速度v1:v2=5:4进行分析,其中P= =
= =Fv,因为由3段绳子承担物重,绳端速度是物体上升速度的3倍;
=Fv,因为由3段绳子承担物重,绳端速度是物体上升速度的3倍;
(2)对物体A在水中和在水外时对物体E、行走装置及杠杆进行受力分析,并列出相等的关系式,结合已知条件得出浮力及A的重力与动滑轮之间的关系,代入公式η= ×100%=
×100%= ×100%,求出η2,注意其中的关系F1=
×100%,求出η2,注意其中的关系F1= (GA-F浮+G动),F2=
(GA-F浮+G动),F2= (GA+G动).
(GA+G动).
(3)由杠杆平衡条件列出2个关系式,结合(2)中的分析得出N1、N2与动滑轮重力的关系,求出其比值.
解答:解:(1)电动机输出功率恒定,∴F13v1=F23v2,其中v1:v2=5:4,
∴F1:F2=4:5
(2)当物体A完全在水中时,对行走装置、电动机、定滑轮进行受力分析,如图1所示,对E进行受力分析,如图2所示,对杠杆进行受力分析,如图3所示:



则:FM1′=GK+3F1,N1+FD1′=GE,FD1?OD=FM1?OM,
其中FM1′=FM1,FD1′=FD1,η1=87.5%,OD:OM=1:2,
F1= (G动+GA-F浮)
(G动+GA-F浮)
η1=
当物体A在水外时,对行走装置、电动机、定滑轮进行受力分析,如图4所示,对E进行受力分析,如图5所示,对杠杆进行受力分析,如图6所示:


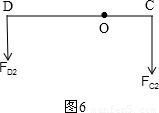
则:FC2′=mKg+3F2,FD2′+N2=GE,FD2?OD=FC2?OC,
其中FC2′=FC2,FD2′=FD2,OD:OC=5:2,
且:VA=2VE,ρE=6ρA,得GE=3GA,F1:F2=4:5,得:
GA=9G动,F浮=2G动,
∴η2= ×100%=
×100%= ×100%=
×100%= ×100%=90%;
×100%=90%;
(3)由(2)中关系式知,
(GE-N1)OD=(GK+3F1)OM,
(GE-N2)OD=(GK+3F2)OC,
OD:OM=1:2,OD:OC=5:2,GA=9G动,F浮=2G动,
F1= (GA-F浮+G动),F2=
(GA-F浮+G动),F2= (GA+G动)
(GA+G动)
则N1=6G动,N2=22G动
∴N1:N2=6:22=3:11
答:(1)打捞前后提升电动机绳子的拉力F1与F2的比值是4:5;
(2)货物A打捞出水后的机械效率是90%;
(3)货物A出水前后地板对配重E的支持力N1与N2的比值是3:11.
点评:本题为力学综合题,考查了学生对重力公式、密度公式、功率公式、效率公式、杠杆平衡条件的掌握和运用,知识点多、综合性强,要求灵活运用所学知识,画出受力示意图帮助解题是本题的关键.
 =
= =Fv,因为由3段绳子承担物重,绳端速度是物体上升速度的3倍;
=Fv,因为由3段绳子承担物重,绳端速度是物体上升速度的3倍;(2)对物体A在水中和在水外时对物体E、行走装置及杠杆进行受力分析,并列出相等的关系式,结合已知条件得出浮力及A的重力与动滑轮之间的关系,代入公式η=
 ×100%=
×100%= ×100%,求出η2,注意其中的关系F1=
×100%,求出η2,注意其中的关系F1= (GA-F浮+G动),F2=
(GA-F浮+G动),F2= (GA+G动).
(GA+G动).(3)由杠杆平衡条件列出2个关系式,结合(2)中的分析得出N1、N2与动滑轮重力的关系,求出其比值.
解答:解:(1)电动机输出功率恒定,∴F13v1=F23v2,其中v1:v2=5:4,
∴F1:F2=4:5
(2)当物体A完全在水中时,对行走装置、电动机、定滑轮进行受力分析,如图1所示,对E进行受力分析,如图2所示,对杠杆进行受力分析,如图3所示:



则:FM1′=GK+3F1,N1+FD1′=GE,FD1?OD=FM1?OM,
其中FM1′=FM1,FD1′=FD1,η1=87.5%,OD:OM=1:2,
F1=
 (G动+GA-F浮)
(G动+GA-F浮)η1=

当物体A在水外时,对行走装置、电动机、定滑轮进行受力分析,如图4所示,对E进行受力分析,如图5所示,对杠杆进行受力分析,如图6所示:



则:FC2′=mKg+3F2,FD2′+N2=GE,FD2?OD=FC2?OC,
其中FC2′=FC2,FD2′=FD2,OD:OC=5:2,
且:VA=2VE,ρE=6ρA,得GE=3GA,F1:F2=4:5,得:
GA=9G动,F浮=2G动,
∴η2=
 ×100%=
×100%= ×100%=
×100%= ×100%=90%;
×100%=90%;(3)由(2)中关系式知,
(GE-N1)OD=(GK+3F1)OM,
(GE-N2)OD=(GK+3F2)OC,
OD:OM=1:2,OD:OC=5:2,GA=9G动,F浮=2G动,
F1=
 (GA-F浮+G动),F2=
(GA-F浮+G动),F2= (GA+G动)
(GA+G动)则N1=6G动,N2=22G动
∴N1:N2=6:22=3:11
答:(1)打捞前后提升电动机绳子的拉力F1与F2的比值是4:5;
(2)货物A打捞出水后的机械效率是90%;
(3)货物A出水前后地板对配重E的支持力N1与N2的比值是3:11.
点评:本题为力学综合题,考查了学生对重力公式、密度公式、功率公式、效率公式、杠杆平衡条件的掌握和运用,知识点多、综合性强,要求灵活运用所学知识,画出受力示意图帮助解题是本题的关键.

练习册系列答案
相关题目
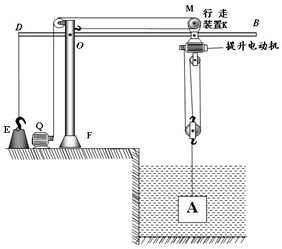 (2012?怀柔区二模)如图是某港口卸载货物的简易装置示意图.该装置由悬挂机构、提升装置和行走装置三部分组成.悬挂机构由固定杆OF和杠杆BD构成,O为杠杆DB的支点.配重E通过绳子竖直拉着杠杆D端,行走装置K安装在杠杆DB上,电动机Q可以使其沿BO水平滑动,行走装置和提升电动机及定滑轮的总质量mK是动滑轮质量的2.5倍.当行走装置处于杠杆DB上M点的位置时,提升电动机拉动绳子,通过滑轮组竖直打捞落入水中的货物A.A完全在水中匀速上升的过程中,提升电动机绳子的拉力为F1,滑轮组的机械效率为η1=87.5%,OD:OM=1:2,地板对配重E的支持力为N1;A全部露出水面匀速竖直上升的过程中,提升电动机绳子的拉力为F2,滑轮组的机械效率为η2,当A静止后,电动机Q启动,水平向左拉动行走装置至点C(图中未标出),使物体静止在海岸上方,以方便卸载货物,此时OD:OC=5:2,地板对配重E的支持力为N2.滑轮组提升A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置平衡.已知提升电动机输出功率恒定,A在水中与出水后匀速运动速度v1:v2=5:4,A的体积是配重E的体积的2倍,配重E的金属密度是物体A的密度的6倍,细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg.求:
(2012?怀柔区二模)如图是某港口卸载货物的简易装置示意图.该装置由悬挂机构、提升装置和行走装置三部分组成.悬挂机构由固定杆OF和杠杆BD构成,O为杠杆DB的支点.配重E通过绳子竖直拉着杠杆D端,行走装置K安装在杠杆DB上,电动机Q可以使其沿BO水平滑动,行走装置和提升电动机及定滑轮的总质量mK是动滑轮质量的2.5倍.当行走装置处于杠杆DB上M点的位置时,提升电动机拉动绳子,通过滑轮组竖直打捞落入水中的货物A.A完全在水中匀速上升的过程中,提升电动机绳子的拉力为F1,滑轮组的机械效率为η1=87.5%,OD:OM=1:2,地板对配重E的支持力为N1;A全部露出水面匀速竖直上升的过程中,提升电动机绳子的拉力为F2,滑轮组的机械效率为η2,当A静止后,电动机Q启动,水平向左拉动行走装置至点C(图中未标出),使物体静止在海岸上方,以方便卸载货物,此时OD:OC=5:2,地板对配重E的支持力为N2.滑轮组提升A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置平衡.已知提升电动机输出功率恒定,A在水中与出水后匀速运动速度v1:v2=5:4,A的体积是配重E的体积的2倍,配重E的金属密度是物体A的密度的6倍,细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg.求: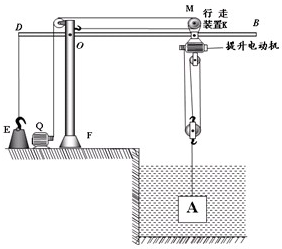 如图是某港口卸载货物的简易装置示意图.该装置由悬挂机构、提升装置和行走装置三部分组成.悬挂机构由固定杆OF和杠杆BD构成,O为杠杆DB的支点.配重E通过绳子竖直拉着杠杆D端,行走装置K安装在杠杆DB上,电动机Q可以使其沿BO水平滑动,行走装置和提升电动机及定滑轮的总质量mK是动滑轮质量的2.5倍.当行走装置处于杠杆DB上M点的位置时,提升电动机拉动绳子,通过滑轮组竖直打捞落入水中的货物A.A完全在水中匀速上升的过程中,提升电动机绳子的拉力为F1,滑轮组的机械效率为η1=87.5%,OD:OM=1:2,地板对配重E的支持力为N1;A全部露出水面匀速竖直上升的过程中,提升电动机绳子的拉力为F2,滑轮组的机械效率为η2,当A静止后,电动机Q启动,水平向左拉动行走装置至点C(图中未标出),使物体静止在海岸上方,以方便卸载货物,此时OD:OC=5:2,地板对配重E的支持力为N2.滑轮组提升A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置平衡.已知提升电动机输出功率恒定,A在水中与出水后匀速运动速度v1:v2=5:4,A的体积是配重E的体积的2倍,配重E的金属密度是物体A的密度的6倍,细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg.求:
如图是某港口卸载货物的简易装置示意图.该装置由悬挂机构、提升装置和行走装置三部分组成.悬挂机构由固定杆OF和杠杆BD构成,O为杠杆DB的支点.配重E通过绳子竖直拉着杠杆D端,行走装置K安装在杠杆DB上,电动机Q可以使其沿BO水平滑动,行走装置和提升电动机及定滑轮的总质量mK是动滑轮质量的2.5倍.当行走装置处于杠杆DB上M点的位置时,提升电动机拉动绳子,通过滑轮组竖直打捞落入水中的货物A.A完全在水中匀速上升的过程中,提升电动机绳子的拉力为F1,滑轮组的机械效率为η1=87.5%,OD:OM=1:2,地板对配重E的支持力为N1;A全部露出水面匀速竖直上升的过程中,提升电动机绳子的拉力为F2,滑轮组的机械效率为η2,当A静止后,电动机Q启动,水平向左拉动行走装置至点C(图中未标出),使物体静止在海岸上方,以方便卸载货物,此时OD:OC=5:2,地板对配重E的支持力为N2.滑轮组提升A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置平衡.已知提升电动机输出功率恒定,A在水中与出水后匀速运动速度v1:v2=5:4,A的体积是配重E的体积的2倍,配重E的金属密度是物体A的密度的6倍,细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg.求: