Question

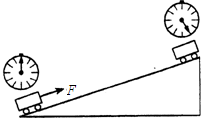（2013?河东区二模）如图实验装置，斜面长2m，高0.5m，秒表每格1s．重为1N的小车在沿斜面方向、大小是0.3N的拉力F作用下，从底端匀速到达顶端，秒表变化如图（指针转动未超过一周）．则（　　）

A．拉力的功率为0.6W

B．斜面的机械效率约为83%

C．拉力所做的功是有用功的1.2倍

D．拉力所做功的功率是有用功的功率的0.1倍

Answer 1

分析：（1）小车在拉力的作用下从底端匀速到达顶端，从而可知小车在拉力的方向上移动的距离，已知拉力的大小，可利用公式W=FS计算拉力所做的功；
（2）从图可知，秒表的指针转动了5个格，秒表每格1s，从而可知做功所需要的时间，再利用公式P=

W

t

计算拉力的功率和有用功率；
（3）从图可知，拉力所做的功为总功，克服重力所做的功为有用功，已知小车的重力和小车上升的高度，可利用公式W=Gh计算有用功，最后利用公式η=

W有用

W总

计算机械效率．

解答：解：（1）∵F=0.3N，S=2m，
∴W=FS=0.3N×2m=0.6J；
∵秒表的指针转动了5个格，做功所需要的时间为：5×1s=5s，
∴P=

W

t

=

0.6J

5s

=0.12W；故A错误；
（2）拉力所做的功为总功，W_总=W=0.6J，
∵G=1N，h=0.5m，
∴W_有用=Gh=1N×0.5m=0.5J，
从而可知，η=

W有用

W总

=

0.5J

0.6J

=83%；故B正确；
（3）

W总

W有用

=

0.6J

0.5J

=1.2；故C正确；
（4）有用功率P_有用=

W有用

t

=

0.5J

5s

=0.1W；
所以

P总

P有用

=

0.12W

0.1W

=1.2，故D错误．
故选B、C．

点评：本题为机械效率的题目，要准确的找到有用功和总功，并可以利用公式进行计算，然后再由时间求出功率，需要注意的是，在计算功率时，要注意所求的为有用功率还是总功率，防止把W代错．