Question

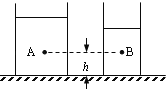
【题目】正方体投入装有水的柱形容器中后漂浮（水未溢出），浸入液体的体积为0.001m3：

（1）求物体所受的浮力_____；

（2）在计算放入物体以后，容器底部所受液体压强的增加量△p液时，小王同学认为：应该用该物体所受的浮力除以容器底面积，即；小红同学认为：应该测量出物体所受的重力，除以容器的底面积，即。你认为，小王同学的观点是_________的，小红同学的观点是_________的。（均选填“正确”或者“错误”）

Answer 1

【答案】9.8N 正确 错误

【解析】

已知物体排开液体的体积，根据阿基米德原理计算物体所受浮力；柱形容器的体积公式为V=Sh；液体压强计算公式为，知道液体的深度h和液体的密度ρ，可计算液体受到的压强，由此来推断观点。

[1] 正方体排开水的体积V排=10-3m3，由阿基米德原理得，物体受到水的浮力：

；

[2][3] 由液体压强公式可知，要得到容器底部所受液体压强的增加量△p液时，需要知道液体变化的深度△h，柱形容器的体积公式为V=Sh，所以：

即：

所以小王同学的观点是正确的。又因为只有物体漂浮或悬浮时，受到浮力大小才等于物体的重力，所以小红同学的观点是错误的。