题目内容
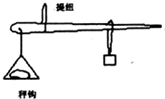 一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g,用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才在水平位置平衡?若秤杆长60cm,则这把秤最大能称量多少kg的物体?(如图所示,秤钩可以认为在最左端处)
一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g,用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才在水平位置平衡?若秤杆长60cm,则这把秤最大能称量多少kg的物体?(如图所示,秤钩可以认为在最左端处)分析:杆秤的提纽是支点,物体重力与秤砣重力分别是动力与阻力,根据题意求出动力臂与阻力臂,根据题意求出动力臂,然后应用杠杆平衡条件可以解题.
解答:解:(1)称质量是2kg的物体时,
由杠杆平衡条件得:G物体×L物体=G秤砣×L秤砣,
m物体g×L物体=m秤砣g×L秤砣,
即2kg×4cm=0.25kg×L秤砣,
解得:L秤砣=32cm;
(2)秤砣在最右端时,秤砣重力的力臂最大,
为L秤砣′=60cm-4cm=56cm,此时所称物体的质量最大,
由杠杆平衡条件得:G物体′×L物体=G秤砣×L秤砣′,
m物体′g×L物体=m秤砣g×L秤砣′,
即:m物体′×4cm=0.25kg×56cm,
解得:m物体′=3.5kg.
答:用来称质量是2kg的物体,秤砣应离提纽32cm;
若秤杆长60cm,则这把秤最大能称量3.5kg的物体.
由杠杆平衡条件得:G物体×L物体=G秤砣×L秤砣,
m物体g×L物体=m秤砣g×L秤砣,
即2kg×4cm=0.25kg×L秤砣,
解得:L秤砣=32cm;
(2)秤砣在最右端时,秤砣重力的力臂最大,
为L秤砣′=60cm-4cm=56cm,此时所称物体的质量最大,
由杠杆平衡条件得:G物体′×L物体=G秤砣×L秤砣′,
m物体′g×L物体=m秤砣g×L秤砣′,
即:m物体′×4cm=0.25kg×56cm,
解得:m物体′=3.5kg.
答:用来称质量是2kg的物体,秤砣应离提纽32cm;
若秤杆长60cm,则这把秤最大能称量3.5kg的物体.
点评:本题考查了杠杆平衡条件的应用,应用杠杆平衡条件即可正确解题,准确求出各力对应的力臂是解题的关键.

练习册系列答案
相关题目
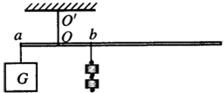 一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g.用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm,则这把秤最大能称量多少千克的物体?
一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g.用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm,则这把秤最大能称量多少千克的物体?