题目内容
一位同学用易拉罐做小孔成像实验．
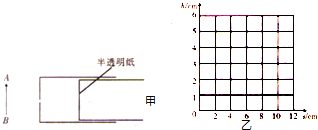
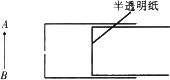
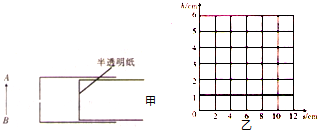
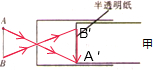
（1）请在甲图中做出蜡烛AB的像
（2）发现蜡烛和小孔的位置固定后，半透明纸离小孔越近，像就越大他测出了不同距离时像的高度，记录在下面的表格中：
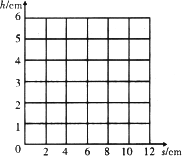
请你根据表中的数据在图乙所示的坐标中划出h与s的关系图象．
（3）从图象中可以看出h与s的关系为
（4）知道树荫下的圆形光斑就是太阳通过树叶的小孔在地面上成的像，他测出了光斑的直径为7.0cm，光斑到小孔的距离为7.5m，从书上查到从太阳到地球的距离为1.5×1011 m，由此可估算出太阳的直径为
（1）请在甲图中做出蜡烛AB的像
（2）发现蜡烛和小孔的位置固定后，半透明纸离小孔越近，像就越大他测出了不同距离时像的高度，记录在下面的表格中：
| 像的高度h/cm | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
| 像到小孔的距离s/cm | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 |
（3）从图象中可以看出h与s的关系为
正比关系
正比关系
．（4）知道树荫下的圆形光斑就是太阳通过树叶的小孔在地面上成的像，他测出了光斑的直径为7.0cm，光斑到小孔的距离为7.5m，从书上查到从太阳到地球的距离为1.5×1011 m，由此可估算出太阳的直径为
1.4×109
1.4×109
m．（可根据几何相似三角形求解）分析：（1）蜡烛AB经过小孔会成倒立的实像，根据光的直线传播原理进行作图；
（2）根据表格中的数据在坐标系中描点，然后用平滑的曲线联起来；
（3）根据正比例函数图象判断h与s的关系；
（4）根据像的直径和像到小孔的距离的比值等于物体的直径和物体到小孔的距离的比值，列式求解．
（2）根据表格中的数据在坐标系中描点，然后用平滑的曲线联起来；
（3）根据正比例函数图象判断h与s的关系；
（4）根据像的直径和像到小孔的距离的比值等于物体的直径和物体到小孔的距离的比值，列式求解．
解答：解：（1）小孔成像是光的直线传播现象．物体上部的光线通过小孔后，射到了光屏的下部；物体下部的光线通过小孔后，射到了光屏的上部，因此通过小孔后所成的像是倒立的像．如图所示：
（2）根据表格中的数据在坐标系中描点，并用平滑的曲线联起来；如下图所示：
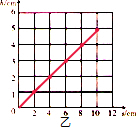
（3）从图象中可以看出h与s的关系为正比关系；
（4）光斑的直径与光斑到小孔的距离的比值是一个定值，根据光线传播的可逆性可知太阳直径和太阳与小孔之间的距离的比值是一个定值，且和光斑的直径与光斑到小孔的距离的比值相等，
所以，太阳的直径d=
×1.5×1011m=1.4×109m．
故答案为：（3）正比关系；（4）1.4×109．
（2）根据表格中的数据在坐标系中描点，并用平滑的曲线联起来；如下图所示：
（3）从图象中可以看出h与s的关系为正比关系；
（4）光斑的直径与光斑到小孔的距离的比值是一个定值，根据光线传播的可逆性可知太阳直径和太阳与小孔之间的距离的比值是一个定值，且和光斑的直径与光斑到小孔的距离的比值相等，
所以，太阳的直径d=
| 0.07m |
| 7.5m |
故答案为：（3）正比关系；（4）1.4×109．
点评：本题考查的是小孔成像的知识，第四问是难点，要用物体所成像的直径和像到小孔距离的比值是一个定值来解答．
练习册系列答案
相关题目
小明同学用易拉罐做小孔成像实验，他在空易拉罐底部的中央，用钉子戳一个小孔，将易拉罐的顶部剪去后，蒙上一层半透明塑料薄膜．
小明同学用易拉罐做小孔成像实验，他在空易拉罐底部的中央，用钉子戳一个小孔，将易拉罐的顶部剪去后，蒙上一层半透明塑料薄膜。
（1）小明把易拉罐正对着点燃的蜡烛(如右图所示)，则在半透明纸上会看到蜡烛的______（选填“正立”或“倒立”）的像，这现象可用光的_________________知识解释．
（2）小明实验时发现小孔成像的大小会变化，于是他设计实验探究小孔所成像的大与哪些因素有关。他猜想所成像的大小可能与蜡烛到小孔的距离、物体的高度以及像到小孔的距离有关。于是他用同一支蜡烛实验，且保持蜡烛到小孔的距离不变，在多次改变小孔到半透明纸之间的距离时，他测出了像的高度（见下表）．
|
小孔到半透明纸的距离s／cm |
2.0 |
4.0 |
6.0 |
8.0 |
10.0 |
|
像的高度h／cm |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
从表格中可以看出：当蜡烛和小孔的距离保持不变时，半透明纸离小孔越远，所成的像越_________。请你根据有关结论判断：当半透明纸距小孔13 cm时，像的高度是________cm．
（3）通过实验，小明得到了正确的结论后很高兴．但他又想，像的大小会不会跟蜡烛离小孔的距离有关呢?在设计这个实验时小明应注意控制___________________、______________________不变。
