题目内容
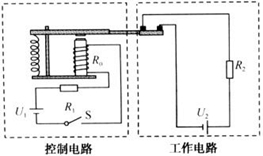 (2011?如皋市一模)小明在研究性学习活动中,查阅到一种热敏电阻的阻值随温度变化的规律如下表,并将该型号的热敏电阻应用于如图所示由“控制电路”和“工作电路”组成的恒温箱电路中.
(2011?如皋市一模)小明在研究性学习活动中,查阅到一种热敏电阻的阻值随温度变化的规律如下表,并将该型号的热敏电阻应用于如图所示由“控制电路”和“工作电路”组成的恒温箱电路中.| 温度/℃ | … | 30 | 40 | 50 | 60 | 70 | … |
| 热敏电阻阻值/Ω | … | 350 | 300 | 250 | 210 | 175 | … |
(1)图中用到哪些物理知识,请说出两点.
电流的磁效应
电流的磁效应
,杠杆的原理
杠杆的原理
.(2)工作电路工作时的电流为多大?电阻R2的发热功率为多大?
(3)若发热电阻R2需提供1.2×104J的热量,则工作电路需工作多长时间(不计热量的损失)?
(4)若恒温箱的温度最高不得超过50℃,则控制电路的电源电压U1最小值为多大?
分析:(1)根据图示的结构:杠杆、电磁铁可以联系到对应的物理知识.
(2)根据工作电路的电源电压和发热电阻的阻值,利用欧姆定律可以求得电路中的电流;利用功率的计算公式可以求得发热功率.
(3)利用求得的发热功率和需要的热量,可以求得工作电路的工作时间.
(4)选取50℃时,热敏电阻R1对应的阻值250Ω为电路中的R1的阻值,根据电路的特点,求出电路的总电阻;结合继电器的衔铁被吸合时,电路中的最小电流,可以求得控制电路中的最小电源电压.
(2)根据工作电路的电源电压和发热电阻的阻值,利用欧姆定律可以求得电路中的电流;利用功率的计算公式可以求得发热功率.
(3)利用求得的发热功率和需要的热量,可以求得工作电路的工作时间.
(4)选取50℃时,热敏电阻R1对应的阻值250Ω为电路中的R1的阻值,根据电路的特点,求出电路的总电阻;结合继电器的衔铁被吸合时,电路中的最小电流,可以求得控制电路中的最小电源电压.
解答:解:(1)控制电路中的电磁继电器里面的构造中有电磁铁,所以用到了电流的磁效应;
有杠杆,涉及了杠杆的原理.
(2)工作电路中,电源电压U2=10V,发热电阻R2=5Ω,工作电路工作时的电流:I2=
=
=2A;
电阻R2的发热功率P2=U2I2=10 V×2 A=20 W.
(3)发热电阻工作时产生的热量:Q=1.2×104J,发热电阻的功率P2=20 W.
所以发热电阻工作时间:t=
=
=6OOs.
(4)当R1温度为50℃时,其阻值R1=250Ω,
∵R1和R0串联,R0=50Ω,
∴R总=R1+R0=250Ω+50Ω=300Ω,
电路的最小工作电流:I1=20mA=0.02A,
因此,控制电路的最小电压为:U1=I1R总=0.02 A×300Ω=6 V.
答:(1)图中用到物理知识:电流的磁效应;杠杆的原理.
(2)工作电路工作时的电流为2A.电阻R2的发热功率为20W.
(3)若发热电阻R2需提供1.2×104J的热量,则工作电路需工作6OOs.
(4)恒温箱的温度最高不得超过50℃,则控制电路的电源电压U1最小值为6V.
有杠杆,涉及了杠杆的原理.
(2)工作电路中,电源电压U2=10V,发热电阻R2=5Ω,工作电路工作时的电流:I2=
| U2 |
| R2 |
| 10V |
| 5Ω |
电阻R2的发热功率P2=U2I2=10 V×2 A=20 W.
(3)发热电阻工作时产生的热量:Q=1.2×104J,发热电阻的功率P2=20 W.
所以发热电阻工作时间:t=
| Q |
| P2 |
| 1.2×104J |
| 20W |
(4)当R1温度为50℃时,其阻值R1=250Ω,
∵R1和R0串联,R0=50Ω,
∴R总=R1+R0=250Ω+50Ω=300Ω,
电路的最小工作电流:I1=20mA=0.02A,
因此,控制电路的最小电压为:U1=I1R总=0.02 A×300Ω=6 V.
答:(1)图中用到物理知识:电流的磁效应;杠杆的原理.
(2)工作电路工作时的电流为2A.电阻R2的发热功率为20W.
(3)若发热电阻R2需提供1.2×104J的热量,则工作电路需工作6OOs.
(4)恒温箱的温度最高不得超过50℃,则控制电路的电源电压U1最小值为6V.
点评:在第四问中,热敏电阻的阻值由很多个,如何选取热敏电阻的阻值是解决此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?如皋市一模)电动机和发电机在构造上差异不大,一个玩具电动机,像图a那样接上电源会转动,像图b那样让其转动起来,可以使小灯泡发光.图b中利用的工作原理是
(2011?如皋市一模)电动机和发电机在构造上差异不大,一个玩具电动机,像图a那样接上电源会转动,像图b那样让其转动起来,可以使小灯泡发光.图b中利用的工作原理是
 (2011?如皋市一模)如图所示,重为G的小铁块在水平方向力F的作用下,沿条形磁铁的表面以直线从N极匀速滑到S极,下列关于F大小的说法正确的是( )
(2011?如皋市一模)如图所示,重为G的小铁块在水平方向力F的作用下,沿条形磁铁的表面以直线从N极匀速滑到S极,下列关于F大小的说法正确的是( )