题目内容
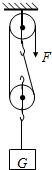 用如图所示的滑轮组,使质量为0.27kg的铝块从空中匀速下落到盛有水的容器中.当铝块接触水面之前,滑轮组的机械效率是54%,(不计绳重和轴处摩擦,g取10N/kg,ρ铝=2.7×103kg/m3)求:
用如图所示的滑轮组,使质量为0.27kg的铝块从空中匀速下落到盛有水的容器中.当铝块接触水面之前,滑轮组的机械效率是54%,(不计绳重和轴处摩擦,g取10N/kg,ρ铝=2.7×103kg/m3)求:(1)当铝块浸没在水中时,滑轮组对铝块的拉力为多少?
(2)铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率是多少?
(3)当铝块浸没在密度为ρ的某种液体中,以0.1m/s的速度匀速下降时,滑轮组绳自由端拉力F的功率为0.42W,液体的密度是多大?
分析:(1)滑轮组对铝块的拉力等于铝块的重力减去铝块受到的浮力;
(2)先根据滑轮组在空中的机械效率解出动滑轮的重力,再用公式η=
=
求出铝块浸没水中匀速下降时滑轮组的机械效率;
(3)先根据绳子股数n求出自由端绳子运动的速度V=nV铝块,由功率公式P=FV求出自由端绳子的拉力,根据绳子股数n求出滑轮组对铝块的拉力,进而求出铝块浸没在某液体中时受到的浮力,从而根据阿基米德F浮=ρ液gV排原理求出待测液体的密度.
(2)先根据滑轮组在空中的机械效率解出动滑轮的重力,再用公式η=
| W有用 |
| W总 |
| F拉 |
| F拉+ G动 |
(3)先根据绳子股数n求出自由端绳子运动的速度V=nV铝块,由功率公式P=FV求出自由端绳子的拉力,根据绳子股数n求出滑轮组对铝块的拉力,进而求出铝块浸没在某液体中时受到的浮力,从而根据阿基米德F浮=ρ液gV排原理求出待测液体的密度.
解答:解:(1)铝块的重力G=mg=0.27kg×10N/kg=2.7N,
铝块的体积V铝=
=
=1.0×10-4m3,
铝块受到的浮力F浮=ρ水 gV排=1.0×103kg/m3×10N/kg×1.0×10-4m3=1N,
滑轮组对铝块的拉力F拉=G-F浮=2.7N-1N=1.7N;
答:当铝块浸没在水中时,滑轮组对铝块的拉力为1.7N.
(2)铝块在空中时满足η=
=
=54%,
解得动滑轮重力G动=2.3N,
铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率
η′=
=
=
=42.5%;
答:铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率为42.5%.
(3)滑轮组绳子的股数n=2,
铝块浸没在密度为ρ的某种液体中,以0.1m/s的速度匀速下降时,绳子自由端运动的速度vF=0.1m/s×2=0.2m/s,
绳子自由端的拉力F=
=
=2.1N,
滑轮组对铝块的拉力F拉′=2F-G动=2×2.1N-2.3N=1.9N,
此时铝块受到的浮力F浮′=G-F拉′=2.7N-1.9N=0.8N,
液体的密度ρ=
=
=0.8×103kg/m3.
答:液体的密度为0.8×103kg/m3.
铝块的体积V铝=
| m |
| ρ铝 |
| 0.27kg |
| 2.7×103kg/m3 |
铝块受到的浮力F浮=ρ水 gV排=1.0×103kg/m3×10N/kg×1.0×10-4m3=1N,
滑轮组对铝块的拉力F拉=G-F浮=2.7N-1N=1.7N;
答:当铝块浸没在水中时,滑轮组对铝块的拉力为1.7N.
(2)铝块在空中时满足η=
| G |
| G+G动 |
| 2.7N |
| 2.7N+G动 |
解得动滑轮重力G动=2.3N,
铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率
η′=
| W有用 |
| W总 |
| F拉 |
| F拉+G动 |
| 1.7N |
| 1.7N+2.3N |
答:铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率为42.5%.
(3)滑轮组绳子的股数n=2,
铝块浸没在密度为ρ的某种液体中,以0.1m/s的速度匀速下降时,绳子自由端运动的速度vF=0.1m/s×2=0.2m/s,
绳子自由端的拉力F=
| P |
| vF |
| 0.42W |
| 0.2m/s |
滑轮组对铝块的拉力F拉′=2F-G动=2×2.1N-2.3N=1.9N,
此时铝块受到的浮力F浮′=G-F拉′=2.7N-1.9N=0.8N,
液体的密度ρ=
| F浮′ |
| gV铝 |
| 0.8N |
| 10N/kg×1.0×10-4m3 |
答:液体的密度为0.8×103kg/m3.
点评:称重法测物体受到的浮力F浮=G-F拉;
物体浸没液体中时滑轮组的机械效率η=
=
;
已知浮力和V排,可用阿基米德原理求某液体密度ρ液=
.
物体浸没液体中时滑轮组的机械效率η=
| W有用 |
| W总 |
| F拉 |
| F拉+G动 |
已知浮力和V排,可用阿基米德原理求某液体密度ρ液=
| F浮 |
| gV排 |

练习册系列答案
相关题目
 10、某人站在地面上,用如图所示的滑轮组竖直向下拉重物使重物匀速上升,不计动滑轮重及摩擦,物重G=1000N,人重G人=600N,则人对绳的拉力是
10、某人站在地面上,用如图所示的滑轮组竖直向下拉重物使重物匀速上升,不计动滑轮重及摩擦,物重G=1000N,人重G人=600N,则人对绳的拉力是 一个工人用如图所示的滑轮组提升2000N的货物,所用拉力为600N,绳子自由端在4s内拉下4m.不计绳重和摩擦,求:
一个工人用如图所示的滑轮组提升2000N的货物,所用拉力为600N,绳子自由端在4s内拉下4m.不计绳重和摩擦,求: (2013?红桥区二模)用如图所示的滑轮组,将重为10N的物体以0.1m/s的速度匀速提升,拉力F=6N,拉力的功率为
(2013?红桥区二模)用如图所示的滑轮组,将重为10N的物体以0.1m/s的速度匀速提升,拉力F=6N,拉力的功率为 用如图所示的滑轮组将重为480N的物体提升1m,所用拉力F为200N.(不计绳重和摩擦)求:
用如图所示的滑轮组将重为480N的物体提升1m,所用拉力F为200N.(不计绳重和摩擦)求: 用如图所示的滑轮组提升重物,每个滑轮重2N,不计绳重和摩擦,若要提起20N的物体,绳子自由端的拉力至少为多少N?
用如图所示的滑轮组提升重物,每个滑轮重2N,不计绳重和摩擦,若要提起20N的物体,绳子自由端的拉力至少为多少N?