题目内容
 一课外小组的同学,通过实验探究:浸没在液体中的物体受到的浮力大小是否跟浸没在液面下的深度有关.如图所示,他们将一高6cm的金属圆柱体挂在弹簧测力计下端,缓慢浸入水中(水足够深且水始终未溢出),在圆柱体接触容器底之前,记下圆柱体下表面所处深度和弹簧测力计相应的拉力,容器底的底面积为30cm2,数据如下表:(g取10N/kg,ρ水=1.0×103 kg/m3)
一课外小组的同学,通过实验探究:浸没在液体中的物体受到的浮力大小是否跟浸没在液面下的深度有关.如图所示,他们将一高6cm的金属圆柱体挂在弹簧测力计下端,缓慢浸入水中(水足够深且水始终未溢出),在圆柱体接触容器底之前,记下圆柱体下表面所处深度和弹簧测力计相应的拉力,容器底的底面积为30cm2,数据如下表:(g取10N/kg,ρ水=1.0×103 kg/m3)| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 深度h/cm | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 拉力F/N | 8.1 | 7.1 | 6.1 | 5.1 | 5.1 | 5.1 | 5.1 |
(2)金属圆柱体的体积是多少?
(3)金属圆柱体的密度是多少?
(4)分析上表数据,求金属圆柱体完全放入水中,水对容器底的压强变化了多少?
分析:(1)金属圆柱体在空气中时,没有受到浮力的作用,弹簧测力计的示数等于它的重力G;金属圆柱体的高度为6cm,完全浸入水中,也就是深度必须在6cm或6cm以下,重力与此时弹簧测力计的示数之差就是金属圆柱体受到的浮力F浮;
(2)金属圆柱体完全浸入水中时,排开水的体积等于它自身的体积,根据(1)中的浮力大小利用公式V排=
就可以计算出;
(3)利用G=mg求出圆柱体的质量,又求出了圆柱体的体积,利用ρ=
就可以算出金属圆柱体的密度.
(4)求出金属圆柱体完全放入水中排开水的体积,利用V=Sh求水面升高值,再根据p=ρgh求水对容器底的压强变化值.
(2)金属圆柱体完全浸入水中时,排开水的体积等于它自身的体积,根据(1)中的浮力大小利用公式V排=
| F浮 |
| ρ水g |
(3)利用G=mg求出圆柱体的质量,又求出了圆柱体的体积,利用ρ=
| m |
| V |
(4)求出金属圆柱体完全放入水中排开水的体积,利用V=Sh求水面升高值,再根据p=ρgh求水对容器底的压强变化值.
解答:解:
(1)序号1中,金属圆柱体没有进入水中,根据二力平衡的知识,此时弹簧测力计的示数等于金属圆柱体的重力,
∴金属圆柱体的重力G=F1=8.1N,
由序号4、5、6、7的数据可知,金属圆柱体完全浸入水中时,弹簧测力计的示数是5.1N,
∴圆柱体受到的浮力F浮=G-F4=8.1N-5.1N=3N;
(2)∵F浮=G排=ρ水gV排,
∴金属圆柱体完全浸入水中时,排开水的体积:
V排=
=
=3×10-4m3,
圆柱体的体积:
V=V排=3×10-4m3;
(3)金属圆柱体的质量m=
=
=0.81kg,
金属圆柱体的体积V=3×10-4m3,
∴金属圆柱体的密度:
ρ=
=
=2.7×103kg/m3;
(4)金属圆柱体完全放入水中排开水的体积:
V排=3×10-4m3,
∵V=Sh,
水面升高值:
△h=
=
=0.1m,
水对容器底的压强变化值:
△p=ρg△h=1×103kg/m3×10N/kg×0.1m=1000Pa.
答:(1)在金属圆柱体完全浸入水中时,其受到的浮力为3N;
(2)金属圆柱体的体积是3×10-4m3;
(3)金属圆柱体的密度是2.7×103kg/m3;
(4)分析上表数据,求金属圆柱体完全放入水中,水对容器底的压强变化了1000Pa.
(1)序号1中,金属圆柱体没有进入水中,根据二力平衡的知识,此时弹簧测力计的示数等于金属圆柱体的重力,
∴金属圆柱体的重力G=F1=8.1N,
由序号4、5、6、7的数据可知,金属圆柱体完全浸入水中时,弹簧测力计的示数是5.1N,
∴圆柱体受到的浮力F浮=G-F4=8.1N-5.1N=3N;
(2)∵F浮=G排=ρ水gV排,
∴金属圆柱体完全浸入水中时,排开水的体积:
V排=
| F浮 |
| ρ水g |
| 3N |
| 1.0×103kg/m3×10N/kg |
圆柱体的体积:
V=V排=3×10-4m3;
(3)金属圆柱体的质量m=
| G |
| g |
| 8.1N |
| 10N/kg |
金属圆柱体的体积V=3×10-4m3,
∴金属圆柱体的密度:
ρ=
| m |
| V |
| 0.81kg |
| 3×10-4m3 |
(4)金属圆柱体完全放入水中排开水的体积:
V排=3×10-4m3,
∵V=Sh,
水面升高值:
△h=
| V排 |
| S |
| 3×10-4m3 |
| 3×10-3m2 |
水对容器底的压强变化值:
△p=ρg△h=1×103kg/m3×10N/kg×0.1m=1000Pa.
答:(1)在金属圆柱体完全浸入水中时,其受到的浮力为3N;
(2)金属圆柱体的体积是3×10-4m3;
(3)金属圆柱体的密度是2.7×103kg/m3;
(4)分析上表数据,求金属圆柱体完全放入水中,水对容器底的压强变化了1000Pa.
点评:(1)用弹簧测力计采用称重法可以测出物体在液体中受到的浮力,根据浮力间接求出体积,这是利用弹簧测力计测密度的基本思路;
(2)探究浮力与计算密度相结合,属综合性题目,中考中经常出现,平时多培养综合处理物理问题的能力.
(2)探究浮力与计算密度相结合,属综合性题目,中考中经常出现,平时多培养综合处理物理问题的能力.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 (2012?射洪县模拟)某物理兴趣小组在课外实践活动中,制作了一个测量质量的电子秤,其原理如图中的虚线框所示,它主要有四部分构成:托盘和压力杠杆ABO,定值电阻R0,压力传感器R(电阻值会随所受压力大小发生变化的可变电阻,它随压力大小的变化关系如右图中的R-F图线),显示质量大小的仪表V(实质是电压表).其中AB:BO=4:1.设托盘和杠杆组件的质量均可忽略不计,电源电压恒为6V.(g取10N/kg)
(2012?射洪县模拟)某物理兴趣小组在课外实践活动中,制作了一个测量质量的电子秤,其原理如图中的虚线框所示,它主要有四部分构成:托盘和压力杠杆ABO,定值电阻R0,压力传感器R(电阻值会随所受压力大小发生变化的可变电阻,它随压力大小的变化关系如右图中的R-F图线),显示质量大小的仪表V(实质是电压表).其中AB:BO=4:1.设托盘和杠杆组件的质量均可忽略不计,电源电压恒为6V.(g取10N/kg)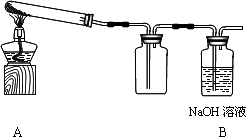

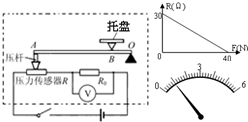 某物理兴趣小组在课外实践活动中,制作了一个测量质量的电子秤,其原理如图中的虚线框所示,它主要有四部分构成:托盘和压力杠杆ABO,定值电阻R0,压力传感器R(电阻值会随所受压力大小发生变化的可变电阻,它随压力大小的变化关系如右图中的R-F图线),显示质量大小的仪表V(实质是电压表).其中AB:BO=4:1.设托盘和杠杆组件的质量均可忽略不计,电源电压恒为6V.(g取10N/kg)
某物理兴趣小组在课外实践活动中,制作了一个测量质量的电子秤,其原理如图中的虚线框所示,它主要有四部分构成:托盘和压力杠杆ABO,定值电阻R0,压力传感器R(电阻值会随所受压力大小发生变化的可变电阻,它随压力大小的变化关系如右图中的R-F图线),显示质量大小的仪表V(实质是电压表).其中AB:BO=4:1.设托盘和杠杆组件的质量均可忽略不计,电源电压恒为6V.(g取10N/kg)