题目内容
 (2013?达州)如图所示,电源电压保持12V不变,L是标有“12V 6W”的小灯泡,其电阻不随温度变化,R=20Ω.
(2013?达州)如图所示,电源电压保持12V不变,L是标有“12V 6W”的小灯泡,其电阻不随温度变化,R=20Ω.(1)当S、S1闭合、S2断开,且P位于滑动变阻器R0的中点时,电流表示数为0.4A.求滑动变阻器R0的最大阻值.
(2)当S、S1、S2都闭合,且P位于a端时,求电流表的示数.
(3)要使电路中的总功率最小,请指出开关S、S1、S2的开闭情况和滑片P的位置,并求出此时的最小功率.
分析:(1)当S、S1闭合、S2断开,且P位于滑动变阻器R0的中点时,灯泡与滑动变阻器阻值的一半串联,电流表测电路中的电流,根据P=
求出灯泡的电阻,再根据电阻的串联求出滑动变阻器的最大阻值;
(2)当S、S1、S2都闭合,且P位于a端时,灯泡与R并联,电流表测干路电流,根据并联电路的电压特点和欧姆定律求出两支路的电流,再根据并联电路的电流特点求出电流表的示数;
(3)当S、S1闭合,S2断开,且P位于b端时,电路中的总电阻最大,根据P=
可知电路中的总功率最小,利用电阻的串联和P=
求出其大小.
| U2 |
| R |
(2)当S、S1、S2都闭合,且P位于a端时,灯泡与R并联,电流表测干路电流,根据并联电路的电压特点和欧姆定律求出两支路的电流,再根据并联电路的电流特点求出电流表的示数;
(3)当S、S1闭合,S2断开,且P位于b端时,电路中的总电阻最大,根据P=
| U2 |
| R |
| U2 |
| R |
解答:解:(1)当S、S1闭合、S2断开,且P位于滑动变阻器R0的中点时,灯泡与滑动变阻器阻值的一半串联,电流表测电路中的电流,
由P=
可得,小灯泡的电阻:
RL=
=
=24Ω,
由欧姆定律可得,电路中的总电阻:
R总=
=
=30Ω,
∵串联电路中总电阻等于各分电阻之和,
R0=R总-RL=30Ω-24Ω=6Ω,
解得:R0=12Ω;
(2)当S、S1、S2都闭合,且P位于a端时,灯泡与R并联,电流表测干路电流,
∵并联电路中各支路两端的电压相等,
∴两支路的电流分别为:
IL=
=
=0.5A,IR=
=
=0.6A,
∵并联电路中干路电流等于各支路电流之和,
∴电流表的示数:
I=IL+IR=0.5A+0.6A=1.1A;
(3)当S、S1闭合,S2断开,且P位于b端时,电路中的总电阻最大,总功率最小,
P最小=
=
=4W.
答:(1)滑动变阻器R0的最大阻值为12Ω;
(2)当S、S1、S2都闭合,且P位于a端时,电流表的示数为1.1A;
(3)当S、S1、S2断开,且P位于b端时,电路中的总功率最小,最小功率为4W.
由P=
| U2 |
| R |
RL=
| U2L |
| PL |
| (12V)2 |
| 6W |
由欧姆定律可得,电路中的总电阻:
R总=
| U |
| I1 |
| 12V |
| 0.4A |
∵串联电路中总电阻等于各分电阻之和,
| 1 |
| 2 |
解得:R0=12Ω;
(2)当S、S1、S2都闭合,且P位于a端时,灯泡与R并联,电流表测干路电流,
∵并联电路中各支路两端的电压相等,
∴两支路的电流分别为:
IL=
| U |
| RL |
| 12V |
| 24Ω |
| U |
| R |
| 12V |
| 20Ω |
∵并联电路中干路电流等于各支路电流之和,
∴电流表的示数:
I=IL+IR=0.5A+0.6A=1.1A;
(3)当S、S1闭合,S2断开,且P位于b端时,电路中的总电阻最大,总功率最小,
P最小=
| U2 |
| RL+R0 |
| (12V)2 |
| 24Ω+12Ω |
答:(1)滑动变阻器R0的最大阻值为12Ω;
(2)当S、S1、S2都闭合,且P位于a端时,电流表的示数为1.1A;
(3)当S、S1、S2断开,且P位于b端时,电路中的总功率最小,最小功率为4W.
点评:本题考查了串联电路的特点和并联电路的特点以及欧姆定律、电功率公式的灵活应用,关键是电路最小电功率的判断.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
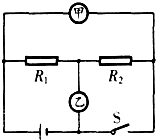 (2013?达州)如图所示,当开关S闭合,甲、乙两表为电压表时,两表读数之比U甲:U乙为4:1;当开关S断开,甲、乙两表为电流表时,两表的读数之比I甲:I乙为( )
(2013?达州)如图所示,当开关S闭合,甲、乙两表为电压表时,两表读数之比U甲:U乙为4:1;当开关S断开,甲、乙两表为电流表时,两表的读数之比I甲:I乙为( )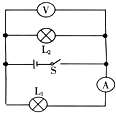 (2013?达州)如图所示,电源电压保持不变,开关S闭合后,灯L1和L2都正常发光,一段时间后,一盏灯突然熄灭,而电压表和电流表示数都不变,则故障原因可能是( )
(2013?达州)如图所示,电源电压保持不变,开关S闭合后,灯L1和L2都正常发光,一段时间后,一盏灯突然熄灭,而电压表和电流表示数都不变,则故障原因可能是( )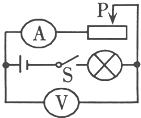 (2013?达州)如图所示,电源电压保持不变,闭合开关S后,滑动变阻器的滑片P向右移动时,电流表A的示数将
(2013?达州)如图所示,电源电压保持不变,闭合开关S后,滑动变阻器的滑片P向右移动时,电流表A的示数将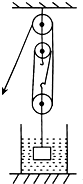 (2013?达州)如图,物体重100N,圆柱形容器底面积为400cm2,内盛有65cm深的水,当用图中滑轮组将物体浸没在水中后,容器中水面上升到70cm,物体完全浸没在水中时滑轮组的机械效率为80%(不计绳重和绳子与滑轮间的摩擦及水的阻力).ρ水=1.0×103kg/m3,g取10N/kg.求:
(2013?达州)如图,物体重100N,圆柱形容器底面积为400cm2,内盛有65cm深的水,当用图中滑轮组将物体浸没在水中后,容器中水面上升到70cm,物体完全浸没在水中时滑轮组的机械效率为80%(不计绳重和绳子与滑轮间的摩擦及水的阻力).ρ水=1.0×103kg/m3,g取10N/kg.求: