题目内容
小明利用杠杆做了两个小实验:
A:“探究杠杆的平衡条件”
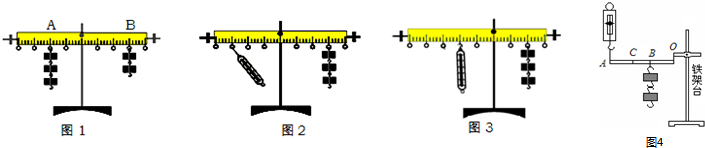
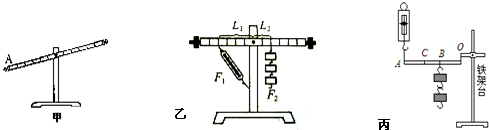
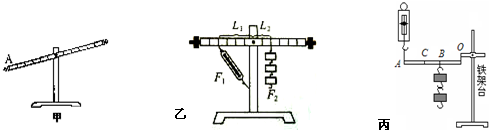
(1)当杆杠静止在图(甲)所示的位置时,杆杠处于
(2)实验中改变支点两侧的钩码位置和个数,用同样的方法一般要做三次,得到三组数据并进行分析.这样做的目的是
(3)在图(乙)中使杠杆处于平衡状态时,测出的拉力大小与杠杆平衡条件不相符.其原因是:
B:“探究杠杆的机械效率”
如图丙所示装置,每个钩码的质量为m,O为支点.
(1)他将2只钩码悬挂在B点,在A点竖直向上匀速拉动弹簧测力计,拉力为F1,测得A、B两点上升的高度分别为h1、h2,则此次杠杆的机械效率为η=
×100%
×100%.(用物理量的符号表示)
(2)他将2只钩码悬挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度为h2,则弹簧测力计的示数将
(3)他将3只钩码悬挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度仍为h2,则第3次杠杆的机械效率与前两次相比
A:“探究杠杆的平衡条件”
(1)当杆杠静止在图(甲)所示的位置时,杆杠处于
平衡
平衡
(“平衡”或“不平衡”)状态,此时应调节杠杆两端的平衡螺母,使杠杆在水平位置平衡,这样做是为了便于测出力臂大小
便于测出力臂大小
;(2)实验中改变支点两侧的钩码位置和个数,用同样的方法一般要做三次,得到三组数据并进行分析.这样做的目的是
使实验结论具有普遍性
使实验结论具有普遍性
.(3)在图(乙)中使杠杆处于平衡状态时,测出的拉力大小与杠杆平衡条件不相符.其原因是:
从杠杆上直接读取不是拉力的力臂
从杠杆上直接读取不是拉力的力臂
.B:“探究杠杆的机械效率”
如图丙所示装置,每个钩码的质量为m,O为支点.
(1)他将2只钩码悬挂在B点,在A点竖直向上匀速拉动弹簧测力计,拉力为F1,测得A、B两点上升的高度分别为h1、h2,则此次杠杆的机械效率为η=
| 2mgh2 |
| F1h1 |
| 2mgh2 |
| F1h1 |
(2)他将2只钩码悬挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度为h2,则弹簧测力计的示数将
大于
大于
(大于/等于/小于)F1,此次弹簧测力计做的功将小于
小于
(大于/等于/小于)第一次做的功.(3)他将3只钩码悬挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度仍为h2,则第3次杠杆的机械效率与前两次相比
最大
最大
(最大/最小/三次相等).
分析:A、(1)杠杆处于静止状态或匀速转动状态时,都杠杆处于平衡状态;探究杠杆平衡条件时,使杠杆在水平位置平衡,力臂在杠杆上,便于测量力臂,同时杠杆的重心通过支点,消除杠杆自重对杠杆平衡的影响.
(2)初中物理用实验探究物理问题时要进行多次实验,有的是为了多次测量求平均值来减小误差;有的是多次测量发现变化规律;有的是为了使实验结论具有普遍性.
(3)杠杆在水平位置平衡时力的方向与杠杆垂直,力臂的长度可以直接从杠杆上读出来.
B、(1)使用杠杆克服钩码的重力做功,有用功等于克服钩码重力做的功,总功等于弹簧测力计的拉力做的功,机械效率等于有用功和总功的比值;
(2)从图中可以看出,将2只钩码悬挂在C点时,重力的力臂大于在B点重力的力臂,而动力臂不变,根据杠杆平衡的条件可知弹簧测力计的示数的变化情况,再分析有用功和额外功的变化,根据总功等于有用功和额外功之和得出弹簧测力计做功的变化情况.
(3)分析有用功、额外功的变化,然后根据机械效率公式即可得出正确结果.
(2)初中物理用实验探究物理问题时要进行多次实验,有的是为了多次测量求平均值来减小误差;有的是多次测量发现变化规律;有的是为了使实验结论具有普遍性.
(3)杠杆在水平位置平衡时力的方向与杠杆垂直,力臂的长度可以直接从杠杆上读出来.
B、(1)使用杠杆克服钩码的重力做功,有用功等于克服钩码重力做的功,总功等于弹簧测力计的拉力做的功,机械效率等于有用功和总功的比值;
(2)从图中可以看出,将2只钩码悬挂在C点时,重力的力臂大于在B点重力的力臂,而动力臂不变,根据杠杆平衡的条件可知弹簧测力计的示数的变化情况,再分析有用功和额外功的变化,根据总功等于有用功和额外功之和得出弹簧测力计做功的变化情况.
(3)分析有用功、额外功的变化,然后根据机械效率公式即可得出正确结果.
解答:解:
A、(1)如图(甲)杠杆处于静止状态,所以杠杆处于平衡状态.但是杠杆右端上翘,没有在水平位置平衡,调节两端的平衡螺母,使杠杆在水平位置平衡,力臂在杠杆上,便于测出力臂大小.
(2)改变支点两侧的钩码位置和个数,一般要做三次实验,得到三组数据并进行分析,得出的实验结论具有普遍性,避免偶然性.
(3)力臂等于支点到力的作用线的距离,当杠杆在水平位置平衡时,拉力的方向与杠杆不垂直,力臂不等于从杠杆标尺刻度上直接读出的,因此测出的拉力大小与杠杆平衡条件不相符,从杠杆上直接读取不是拉力的力臂.
B、(1)有用功为W有=Gh2=2mgh2,总功W总=F1h1,则机械效率的表达式η=
×100%=
×100%.
(2)钩码的悬挂点在B点时,由杠杠的平衡条件得F1?OA=G?OB;悬挂点移至C点时,由杠杠的平衡条件得F2?OA=G?OC;从图中可以看出,由OB到OC力臂变大,所以弹簧测力计的示数变大,有用功不变,但杠杆提升的高度减小,额外功减小,又因为总功等于额外功与有用功之和,因此此次弹簧测力计做的功将小于第一次做的功.
(3)因为第一次与第二次的有用功相等,并且第二次的额外功小,因为机械效率等于有用功与总功的比值,因此第一次的机械效率小于第二次的机械效率;
将3只钩码悬挂在C点时,物体升高的高度不变,物重增加,由W有=Gh2可得,有用功变大,但杠杆提升的高度与第二次相同,额外功与第二次相同,又因为机械效率等于有用功与总功的比值,因此第三次的机械效率大于第二次的机械效率.
综上所述,第三次的机械效率最大.
故答案为:
A、(1)平衡;左;(2)便于测出力臂大小;(3)从杠杆上直接读取不是拉力的力臂.
B、(1)
×100%;(2)大于;小于;(3)最大.
A、(1)如图(甲)杠杆处于静止状态,所以杠杆处于平衡状态.但是杠杆右端上翘,没有在水平位置平衡,调节两端的平衡螺母,使杠杆在水平位置平衡,力臂在杠杆上,便于测出力臂大小.
(2)改变支点两侧的钩码位置和个数,一般要做三次实验,得到三组数据并进行分析,得出的实验结论具有普遍性,避免偶然性.
(3)力臂等于支点到力的作用线的距离,当杠杆在水平位置平衡时,拉力的方向与杠杆不垂直,力臂不等于从杠杆标尺刻度上直接读出的,因此测出的拉力大小与杠杆平衡条件不相符,从杠杆上直接读取不是拉力的力臂.
B、(1)有用功为W有=Gh2=2mgh2,总功W总=F1h1,则机械效率的表达式η=
| W有 |
| W总 |
| 2mgh2 |
| F1h1 |
(2)钩码的悬挂点在B点时,由杠杠的平衡条件得F1?OA=G?OB;悬挂点移至C点时,由杠杠的平衡条件得F2?OA=G?OC;从图中可以看出,由OB到OC力臂变大,所以弹簧测力计的示数变大,有用功不变,但杠杆提升的高度减小,额外功减小,又因为总功等于额外功与有用功之和,因此此次弹簧测力计做的功将小于第一次做的功.
(3)因为第一次与第二次的有用功相等,并且第二次的额外功小,因为机械效率等于有用功与总功的比值,因此第一次的机械效率小于第二次的机械效率;
将3只钩码悬挂在C点时,物体升高的高度不变,物重增加,由W有=Gh2可得,有用功变大,但杠杆提升的高度与第二次相同,额外功与第二次相同,又因为机械效率等于有用功与总功的比值,因此第三次的机械效率大于第二次的机械效率.
综上所述,第三次的机械效率最大.
故答案为:
A、(1)平衡;左;(2)便于测出力臂大小;(3)从杠杆上直接读取不是拉力的力臂.
B、(1)
| 2mgh2 |
| F1h1 |
点评:本题考查杠杆机械效率的测量,把握有用功、总功的计算方式,明确机械效率的表达式,知道总功等于有用功与额外功之和.

练习册系列答案
相关题目