题目内容
小强在探究“杠杆的平衡条件”时,如图1所示:

下面是他所设计的探究“杠杆平衡条件”的步骤:
①把杠杆的中点支在支架上;
②把钩码挂在杠杆两边,改变钩码的位置使杠杆平衡;
③记下两边钩码受到的重力,并用尺量出它们的力臂,
分别填入实验数据的表格内;
④改变力和力臂的数值,做三次实验;
⑤求出各次实验的动力乘以动力臂和阻力乘以阻力臂的数值.
(1)该同学在
(2)下表是小强的实验记录,在这两组数据中,他发现实验有一组数据是错误的.经检查,结果是测量阻力臂时读错了,阻力臂的实际值应为
(3)另一个同学小红根据实验现象得出的杠杆平衡条件是:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”.为了说明这一结论并不正确,请你在图2所示的杠杠B点上画出需要对杠杠施加的力的示意图和这个力的力臂.
(4)如图3所示,绳子OO′悬吊着质量忽略不计的杠杆,在杆的a点挂上重物G,在O右侧某点b处挂上钩码.重 物G的质量及a到O的距离不变,要使杆保持水平,b点挂的钩码个数(各个钩码质量相同)和b到O的距离的关系是图4中哪一幅图.

下面是他所设计的探究“杠杆平衡条件”的步骤:
①把杠杆的中点支在支架上;
②把钩码挂在杠杆两边,改变钩码的位置使杠杆平衡;
③记下两边钩码受到的重力,并用尺量出它们的力臂,
分别填入实验数据的表格内;
④改变力和力臂的数值,做三次实验;
⑤求出各次实验的动力乘以动力臂和阻力乘以阻力臂的数值.
(1)该同学在
第①
第①
步漏掉了一个重要的步骤.这一步写完整应为把杠杆的中点支在支架上,调节杠杆两端的平衡螺母,使杠杆水平平衡
把杠杆的中点支在支架上,调节杠杆两端的平衡螺母,使杠杆水平平衡
.(2)下表是小强的实验记录,在这两组数据中,他发现实验有一组数据是错误的.经检查,结果是测量阻力臂时读错了,阻力臂的实际值应为
0.6
0.6
m.| 实验序号 | 动力F1/N | 动力臂L1/m | 阻力F2/N | 阻力臂L2/m |
| 1 | 2 | 0.3 | 1 | 0.4 |
| 2 | 1 | 0.4 | 2 | 0.2 |
(4)如图3所示,绳子OO′悬吊着质量忽略不计的杠杆,在杆的a点挂上重物G,在O右侧某点b处挂上钩码.重 物G的质量及a到O的距离不变,要使杆保持水平,b点挂的钩码个数(各个钩码质量相同)和b到O的距离的关系是图4中哪一幅图.
分析:(1)在探究杠杆的平衡条件时,首先是杠杆的安装与调平,为了在杠杆上能直接读出力臂的大小,调节其两端的平衡螺母使之在水平位置平衡.
(2)杠杆的平衡条件是:动力×动力臂=阻力×阻力臂,由此判断出数据记录中的错误.
(3)小红得出的杠杆平衡条件是:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”,是在杠杆在水平位置平衡且动力和阻力的方向都是竖直向下的条件下得出的,不一定带有普遍性.因此在此实验中为验证是否是力与支点到力的作用点的距离的乘积,所以再设计一个方向不在竖直方向的拉力杠杆平衡.
(4)根据杠杆平衡条件动力×动力臂=阻力×阻力臂去分析:因为重物G和a点到O的距离不变,所以钩码的重力与b点到O的距离成反比,然后逐一分析所给图象即可.
(2)杠杆的平衡条件是:动力×动力臂=阻力×阻力臂,由此判断出数据记录中的错误.
(3)小红得出的杠杆平衡条件是:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”,是在杠杆在水平位置平衡且动力和阻力的方向都是竖直向下的条件下得出的,不一定带有普遍性.因此在此实验中为验证是否是力与支点到力的作用点的距离的乘积,所以再设计一个方向不在竖直方向的拉力杠杆平衡.
(4)根据杠杆平衡条件动力×动力臂=阻力×阻力臂去分析:因为重物G和a点到O的距离不变,所以钩码的重力与b点到O的距离成反比,然后逐一分析所给图象即可.
解答:解:(1)探究杠杆平衡条件实验时,应先进行的是杠杆的组装与调平,第①步骤中,只描述了杠杆的组装,没有调平的步骤,因此是不完整的;
故答案为:第①、把杠杆的中点支在支架上,调节杠杆两端的平衡螺母,使杠杆水平平衡.
(2)根据杠杆平衡的条件,在第1组实验数据中,2N×0.3m≠1N×0.4m,而是2N×0.3m=1N×0.6m,所以第1组数据错误,阻力臂实际值为0.6m;
故答案为:0.6.
(3)因杠杆仍在水平位置平衡,所以设计的拉力方向不要与杠杆垂直即可,支点到力的作用点的距离不再是力臂,这样做研究杠杆平衡的条件实验,得到结论就不能是:动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离.故杠杠施加的力的示意图和这个力的力臂如图所示:
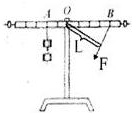 或
或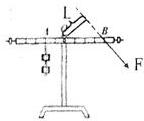
(4)∵重物G和a点到O的距离不变;
∴根据杠杆的平衡条件知:钩码的重力与b点到O的距离的积是一个定值,
即:钩码的重力与b点到O的距离成反比.
要使杆保持水平,b点挂的钩码个数(各个钩码质量相同)和b到O的距离成反比例关系,图象应该是第一象限内的曲线.
故选B.
故答案为:第①、把杠杆的中点支在支架上,调节杠杆两端的平衡螺母,使杠杆水平平衡.
(2)根据杠杆平衡的条件,在第1组实验数据中,2N×0.3m≠1N×0.4m,而是2N×0.3m=1N×0.6m,所以第1组数据错误,阻力臂实际值为0.6m;
故答案为:0.6.
(3)因杠杆仍在水平位置平衡,所以设计的拉力方向不要与杠杆垂直即可,支点到力的作用点的距离不再是力臂,这样做研究杠杆平衡的条件实验,得到结论就不能是:动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离.故杠杠施加的力的示意图和这个力的力臂如图所示:
 或
或
(4)∵重物G和a点到O的距离不变;
∴根据杠杆的平衡条件知:钩码的重力与b点到O的距离的积是一个定值,
即:钩码的重力与b点到O的距离成反比.
要使杆保持水平,b点挂的钩码个数(各个钩码质量相同)和b到O的距离成反比例关系,图象应该是第一象限内的曲线.
故选B.
点评:(1)力臂与支点到力的作用点的距离,不能相提并论,它们相等是有条件的;杠杆在水平位置平衡后,支点到力的作用点的距离就是力臂,因此在此实验中我们应调节杠杆两端的平衡螺母,使杠杆在水平位置平衡,以便直接读出力臂.
(2)杠杆平衡条件的简单应用:动力与动力臂不变时,阻力与阻力臂成反比;阻力与阻力臂不变时,动力与动力臂成反比.处理此类题目时,要找出杠杠的五要素,并确定哪些要素不会发生变化.
(2)杠杆平衡条件的简单应用:动力与动力臂不变时,阻力与阻力臂成反比;阻力与阻力臂不变时,动力与动力臂成反比.处理此类题目时,要找出杠杠的五要素,并确定哪些要素不会发生变化.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目

 小强在探究“杠杆的平衡条件”时:
小强在探究“杠杆的平衡条件”时: (3)下表是小强的实验记录,在这两组数据中,他发现实验序号为
(3)下表是小强的实验记录,在这两组数据中,他发现实验序号为