题目内容
有密度为1克/厘米3的水和密度为0.8克/厘米3的酒精各160克,用它们配制密度为0.84克/厘米3的消毒酒精,最多能配成多少克消毒酒精?(混合过程中体积的变化忽略不计)
解:设取水m1克,取酒精m2克,配成密度为ρ的消毒酒精m克.
∵水和酒精混合后体积不变.
∴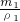 +
+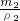 =
= ,
, +
+ =
=
得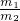 =
=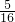
∵m2>m1
故取酒精m2=160g时,水取m1=50g;
最多能配成消毒酒精:
m=m1+m2=50g+160g=210g.
答:最多能配成210g消毒酒精.
分析:设最多能配消毒酒精为m克,需取水m1克,取酒精m2克;根据密度公式和混合过程中体积的变化忽略不计得出消毒酒精的体积;根据比例关系即可求出所需水和酒精的质量,从而求出最多能配消毒酒精的质量.
点评:解决本题的关键是利用密度公式求出水和酒精的质量关系,然后利用比值的关系进行求解.
∵水和酒精混合后体积不变.
∴
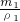 +
+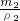 =
= ,
, +
+ =
=
得
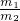 =
=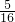
∵m2>m1
故取酒精m2=160g时,水取m1=50g;
最多能配成消毒酒精:
m=m1+m2=50g+160g=210g.
答:最多能配成210g消毒酒精.
分析:设最多能配消毒酒精为m克,需取水m1克,取酒精m2克;根据密度公式和混合过程中体积的变化忽略不计得出消毒酒精的体积;根据比例关系即可求出所需水和酒精的质量,从而求出最多能配消毒酒精的质量.
点评:解决本题的关键是利用密度公式求出水和酒精的质量关系,然后利用比值的关系进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目