题目内容
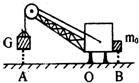在一些建筑工地、港口常见到各种大型起重机．如图所示是一种起重机的简图，为了保证起重机起重时不会翻倒，在起重机右边配有一个重物m0，已知OA=10m，OB=5m，起重机功率为30kW，若不考虑起重机本身重力的影响．求：（1）要使起重机吊起6×103kg的货物时不会绕支点O翻倒，右边的配重m0的质量至少为多少？
（2）如果机械效率为80%，那么，把5×103kg的货物沿竖直方向匀速提高15m，需要多少时间？
分析：（1）以O作为支点，将物重和配重分别看作动力和阻力，已知两力臂OA、OB的长，依据杠杆的平衡条件列式求解即可．
（2）题目给出了货物的质量和提升的高度，可以先求出提升这些货物所做的有用功W有用=Gh=mgh，又知起重机的机械效率，可得提升这些货物所做的总功（W总=
），已知了起重机的功率，根据t=
即可求得所需时间．
（2）题目给出了货物的质量和提升的高度，可以先求出提升这些货物所做的有用功W有用=Gh=mgh，又知起重机的机械效率，可得提升这些货物所做的总功（W总=
| W有用 |
| η |
| W总 |
| P |
解答：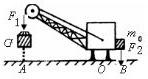
解：（1）F1×OA=F2×OB
mg×OA=m0g×OB
6×103kg×10m=m0×5m
m0=1.2×104kg
答：右边的配重m0的质量至少为1.2×104kg．
（2）t=
=
=
=
=
=31.25s
答：时间为31.25s．
解：（1）F1×OA=F2×OBmg×OA=m0g×OB
6×103kg×10m=m0×5m
m0=1.2×104kg
答：右边的配重m0的质量至少为1.2×104kg．
（2）t=
| W总 |
| P |
| W有用 |
| Pη |
| Gh |
| Pη |
| mgh |
| Pη |
| 5×103kg×10N/kg×15m |
| 3.0×104W×0.8 |
答：时间为31.25s．
点评：本题考查机械效率的计算，杠杆平衡条件及其应用，属于一道好题．
练习册系列答案
相关题目
