题目内容
将边长为10cm的正方体木块平放在圆柱形容器的底部，圆柱形容器的横截面积为300cm2，现缓慢地往容器中注水，当容器中的水面升至8cm时，木块对容器底面的压力恰好为零，g取10N/kg．求
（1）注入水的质量是多少？
（2）木块的密度是多大？
（1）注入水的质量是多少？
（2）木块的密度是多大？
分析：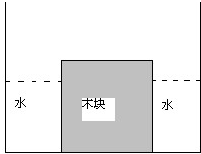
（1）如图所示，要求注入的水的质量，就要求出木块两侧的水的体积，根据公式m=ρv，得注水的质量．
水的体积等于水柱的底面积乘以注入的水的高度．
水柱的底面积等于容器的底面积减去木块的底面积．由此入手可以求得注入的水的质量．
（2）木块的密度可以利用公式：ρ=
，求得．
木块的体积等于边长的立方．
木块此时对容器底的压力为零，所以，木块此时受到的浮力等于木块的重力．
根据阿基米德原理，求得木块受到的浮力，即可求出木块的重力，进而得到木块的质量．从而可以求得木块的密度．
（1）如图所示，要求注入的水的质量，就要求出木块两侧的水的体积，根据公式m=ρv，得注水的质量．水的体积等于水柱的底面积乘以注入的水的高度．
水柱的底面积等于容器的底面积减去木块的底面积．由此入手可以求得注入的水的质量．
（2）木块的密度可以利用公式：ρ=
| G |
| gv |
木块的体积等于边长的立方．
木块此时对容器底的压力为零，所以，木块此时受到的浮力等于木块的重力．
根据阿基米德原理，求得木块受到的浮力，即可求出木块的重力，进而得到木块的质量．从而可以求得木块的密度．
解答：解：（1）木块的底面积：S木=a2=10cm×10cm=100cm2=1×10-2m2．
S底=300cm2=3×10-2m2
注入的水的体积：V水=（S底-S木）h=（3×10-2m2-1×10-2m2）×8×10-2m=1.6×10-3m3
注入的水的质量：m水=ρ水V水=1.0×103kg/m3×1.6×10-3m3=1.6kg
（2）木块排开水的体积：V排=S木h=1×10-2m2×8×10-2m=8×10-4m3
由于木块此时对容器底的压力为零，所以，木块此时受到的浮力等于木块的重力：即G木=F浮=ρ水gV排=1.0×103kg/m3×10N/kg×8×10-4m3=8N
木块的体积：V木=a3=1×10-3m3
木块的密度：ρ木=
=
=0.8×103kg/m3．
故答案为：（1）注入水的质量是1.6kg．
（2）木块的密度是0.8×103kg/m3．
S底=300cm2=3×10-2m2
注入的水的体积：V水=（S底-S木）h=（3×10-2m2-1×10-2m2）×8×10-2m=1.6×10-3m3
注入的水的质量：m水=ρ水V水=1.0×103kg/m3×1.6×10-3m3=1.6kg
（2）木块排开水的体积：V排=S木h=1×10-2m2×8×10-2m=8×10-4m3
由于木块此时对容器底的压力为零，所以，木块此时受到的浮力等于木块的重力：即G木=F浮=ρ水gV排=1.0×103kg/m3×10N/kg×8×10-4m3=8N
木块的体积：V木=a3=1×10-3m3
木块的密度：ρ木=
| G木 |
| gV木 |
| 8N |
| 10N/kg×10-3m3 |
故答案为：（1）注入水的质量是1.6kg．
（2）木块的密度是0.8×103kg/m3．
点评：解决较复杂的物理题，一定要搞清楚各个量之间的关系．在此题中，可以通过画图的方法，把S木、S底、S水三者之间的关系搞清楚．
题目中告诉的：木块对容器底面的压力恰好为零这句话是求解木块的重力关键．
题目中告诉的：木块对容器底面的压力恰好为零这句话是求解木块的重力关键．
练习册系列答案
相关题目
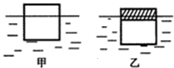（2011?怀柔区）边长为10cm的正立方体木块，漂浮在水面上时，有五分之二的体积露出水面，如图甲所示．将木块截去一部分后，再用少许粘合剂（其质量和体积忽略不计）固定上与截去部分体积相同的合金材料后，投入某种液体中仍漂浮，如图乙所示，此时液体对它竖直向上的压强为1×103 Pa，ρ合金=2.6×103 kg/m3，则合金材料的质量是
，
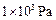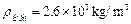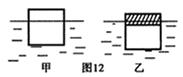
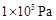，则合金材料的质量是＿＿＿＿＿＿＿kg。（g=10N/kg）
，
，则合金材料的质量是＿＿＿＿＿＿＿kg。（g=10N/kg）
