题目内容
某驾驶员为了粗略测定汽车上货物的质量,采用了这样的办法:让一辆汽车以不变的输出功率P沿一段平直公路匀速行驶,从速度表上读出此时汽车的速度为v.如果汽车运动时受到的阻力与整车重力成正比,比例系数为k,已知汽车自身的质量为M,车上货物的质量设为m.
(1)求货物的质量m;
(2)如果减少货物质量,使整辆车的质量变为原来整辆车质量的9/10,而汽车的输出功率仍为P,汽车原来沿一段平直公路匀速行驶需要10min.那么,减少质量后,汽车匀速经过同一路段需要多少时间?
解:(1)由题知,f=k(m+M)g,
∵P=Fv,
∴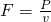 ,
,
∵汽车匀速直线运动
∴F=f,
即: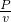 =k(m+M)g,
=k(m+M)g,
∴m= -M;
-M;
(2)设此时汽车的速度为v′,受到的摩擦力为f′,改变质量前后汽车经过同一路段所需时间分别为t和t′,则
f′=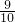 k(m+M)g,
k(m+M)g,
P=f′v′=fv
即: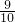 k(m+M)gv′=k(m+M)gv,
k(m+M)gv′=k(m+M)gv,
∴v′= v,
v,
t′= =
= =
=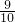 t=
t=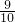 ×10min=9min.
×10min=9min.
答:(1)货物的质量为 -M;
-M;
(2)减少质量后,汽车匀速经过同一路段需要9min.
分析:(1)由题知,汽车运动时受到的阻力与整车重力成正比,且知道比例系数,求出阻力f,
知道汽车的输出功率,且匀速运动(速度为v),利用P=Fv求牵引力F;再根据发F求出货物的质量.
(2)根据(1)中阻力与整车重力的关系,求出此时的阻力,而阻力等于牵引力,根据输出功率不变求出前后车速的关系,再利用速度公式求前后的时间关系,进而求出减少质量后,汽车匀速经过同一路段需要的时间.
点评:本题关键:一是利用好汽车匀速行驶时P=Fv,二是利用好汽车匀速行驶时F=f.
∵P=Fv,
∴
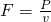 ,
,∵汽车匀速直线运动
∴F=f,
即:
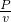 =k(m+M)g,
=k(m+M)g,∴m=
 -M;
-M;(2)设此时汽车的速度为v′,受到的摩擦力为f′,改变质量前后汽车经过同一路段所需时间分别为t和t′,则
f′=
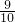 k(m+M)g,
k(m+M)g,P=f′v′=fv
即:
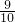 k(m+M)gv′=k(m+M)gv,
k(m+M)gv′=k(m+M)gv,∴v′=
 v,
v,t′=
 =
= =
=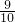 t=
t=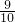 ×10min=9min.
×10min=9min.答:(1)货物的质量为
 -M;
-M;(2)减少质量后,汽车匀速经过同一路段需要9min.
分析:(1)由题知,汽车运动时受到的阻力与整车重力成正比,且知道比例系数,求出阻力f,
知道汽车的输出功率,且匀速运动(速度为v),利用P=Fv求牵引力F;再根据发F求出货物的质量.
(2)根据(1)中阻力与整车重力的关系,求出此时的阻力,而阻力等于牵引力,根据输出功率不变求出前后车速的关系,再利用速度公式求前后的时间关系,进而求出减少质量后,汽车匀速经过同一路段需要的时间.
点评:本题关键:一是利用好汽车匀速行驶时P=Fv,二是利用好汽车匀速行驶时F=f.

练习册系列答案
相关题目