题目内容
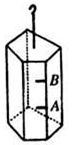
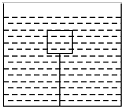
如图所示,将一个体积为1.0×10-3m3、重6N的木块用细线系在底面积为400cm2的圆柱形容器的底部.当容器中倒入足够的水使木块被浸没时,求:(g=10N/kg)
(1)木块浸没在水中受到的浮力;
(2)剪断细线后,木块处于静止时,木块露出水面的体积多大;
(3)木块露出水面处于静止后,容器底部所受水的压强减小了多少.
(1)木块浸没在水中受到的浮力;
(2)剪断细线后,木块处于静止时,木块露出水面的体积多大;
(3)木块露出水面处于静止后,容器底部所受水的压强减小了多少.

(1)木块浸没在水中时受到的浮力:F浮=ρ液gV排=1.0×103kg/m3×10N/kg×1.0×10-3m3=10N;
(2)因为木块浸没在水中时的浮力大于木块的重力,所以剪断细线后,木块会上浮直至漂浮在水面上,
由于漂浮,所以F浮=G=6N,
由F浮=ρ液gV排得:V排=
=
=6×10-4m3,
则V露=V-V排=1.0×10-3m3-6×10-4m3=4×10-4m3;
(3)木块露出水面处于静止后,水面下降的高度:h减=
=
=0.01m,
则容器底部所受水的压强减小了:P=ρ液gh=1.0×103kg/m3×10N/kg×0.01m=100Pa.
答:(1)木块浸没在水中受到的浮力为10N.
(2)剪断细线后,木块处于静止时,木块露出水面的体积为4×10-4m3.
(3)木块露出水面处于静止后,容器底部所受水的压强减小了100Pa.
(2)因为木块浸没在水中时的浮力大于木块的重力,所以剪断细线后,木块会上浮直至漂浮在水面上,
由于漂浮,所以F浮=G=6N,
由F浮=ρ液gV排得:V排=
| F浮 |
| ρ水g |
| 6N |
| 1.0×103kg/m3×10N/kg |
则V露=V-V排=1.0×10-3m3-6×10-4m3=4×10-4m3;
(3)木块露出水面处于静止后,水面下降的高度:h减=
| V露 |
| S容器 |
| 4×10-4m3 |
| 400×10-4m2 |
则容器底部所受水的压强减小了:P=ρ液gh=1.0×103kg/m3×10N/kg×0.01m=100Pa.
答:(1)木块浸没在水中受到的浮力为10N.
(2)剪断细线后,木块处于静止时,木块露出水面的体积为4×10-4m3.
(3)木块露出水面处于静止后,容器底部所受水的压强减小了100Pa.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目