题目内容
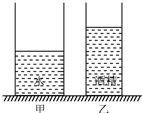 (2013?松江区三模)如图所示,圆柱形容器甲和乙放在水平桌面上,它们的底面积分别为0.02米2和0.01米2.容器甲中盛有0.2米高的水,容器乙中盛有0.3米高的酒精.
(2013?松江区三模)如图所示,圆柱形容器甲和乙放在水平桌面上,它们的底面积分别为0.02米2和0.01米2.容器甲中盛有0.2米高的水,容器乙中盛有0.3米高的酒精.求:(1)容器甲底部受到液体的压强;
(2)容器乙中液体的质量和液体对容器底的压力;
(3)若从两容器中分别抽出质量均为的水和酒精后,剩余水对容器甲底部的压强为p水,剩余酒精对容器乙底部的压强为p酒精.当质量的范围为多少时,才能满足p水>p酒精.(ρ酒精=0.8×103千克/米3)
分析:(1)已知水的深度,根据公式p水=ρ水gh水 可求甲容器中水对容器底部的压强;
(2)已知酒精的深度和容器的底面积,可求酒精的体积,再利用公式m=ρV可求乙容器中酒精的质量.再利用F=pS=ρghS=ρgV=mg求液体对容器底的压力;
(3)因为容器形状规则,液体对容器底部的压力等于自身的重力,当p水>p酒精时,由公式p=
列出一个压强的不等式,进一步求出抽出液体的质量范围.
(2)已知酒精的深度和容器的底面积,可求酒精的体积,再利用公式m=ρV可求乙容器中酒精的质量.再利用F=pS=ρghS=ρgV=mg求液体对容器底的压力;
(3)因为容器形状规则,液体对容器底部的压力等于自身的重力,当p水>p酒精时,由公式p=
| F |
| S |
解答:解:
(1)p水=ρ水gh=1.0×103kg/m3×9.8N/kg×0.2m=1960Pa;
(2)∵ρ=
,
∴m酒精=ρ酒精V酒精=0.8×103kg/m3×0.3m×0.01m2=2.4kg,
∵乙容器为圆柱形容器,
∴液体对容器底的压力:
F=pS=ρghS=ρgV=mg,
∴酒精对容器底的压力:
F酒精=G酒精=m酒精g=2.4kg×9.8N/kg=23.52N;
(3)∵ρ=
,
m水=ρ水V水=1.0×103kg/m3×0.2m×0.02m2=4kg,
设抽出液体的质量为△m,
则甲抽出水后剩余水对容器甲底部的压强:
p水=
=
=
,
乙抽出酒精水后剩余酒精对容器甲底部的压强:
p酒精=
=
=
,
∵p水>p酒精
∴
>
解得:m>0.8kg.
抽出液体的质量范围为:
0.8kg<△m<2.4kg.
答:(1)容器甲底部受到液体的压强为1960Pa;
(2)容器乙中液体的质量为2.4kg,液体对容器底的压力为23.52N;
(3)当抽出液体的质量范围为0.8kg<△m<2.4kg时,才能满足p水>p酒精.
(1)p水=ρ水gh=1.0×103kg/m3×9.8N/kg×0.2m=1960Pa;
(2)∵ρ=
| m |
| V |
∴m酒精=ρ酒精V酒精=0.8×103kg/m3×0.3m×0.01m2=2.4kg,
∵乙容器为圆柱形容器,
∴液体对容器底的压力:
F=pS=ρghS=ρgV=mg,
∴酒精对容器底的压力:
F酒精=G酒精=m酒精g=2.4kg×9.8N/kg=23.52N;
(3)∵ρ=
| m |
| V |
m水=ρ水V水=1.0×103kg/m3×0.2m×0.02m2=4kg,
设抽出液体的质量为△m,
则甲抽出水后剩余水对容器甲底部的压强:
p水=
| F水 |
| S水 |
| (m水-△m)g |
| S水 |
| (4kg-△m)g |
| 0.02m2 |
乙抽出酒精水后剩余酒精对容器甲底部的压强:
p酒精=
| F酒精 |
| S酒精 |
| (m酒精-△m)g |
| S酒精 |
| (2.4kg-△m)g |
| 0.01m2 |
∵p水>p酒精
∴
| 4kg-△m |
| 0.02m2 |
| 2.4kg-△m |
| 0.01m2 |
解得:m>0.8kg.
抽出液体的质量范围为:
0.8kg<△m<2.4kg.
答:(1)容器甲底部受到液体的压强为1960Pa;
(2)容器乙中液体的质量为2.4kg,液体对容器底的压力为23.52N;
(3)当抽出液体的质量范围为0.8kg<△m<2.4kg时,才能满足p水>p酒精.
点评:本题考查液体压强和密度公式的应用,难点是根据压强关系求出抽取液体的质量范围.

练习册系列答案
相关题目
 (2013?松江区三模)在图所示的电路中,电源电压保持不变.闭合电键S,当滑动 变阻器的滑片P向左移动时,电流表A的示数将
(2013?松江区三模)在图所示的电路中,电源电压保持不变.闭合电键S,当滑动 变阻器的滑片P向左移动时,电流表A的示数将 (2013?松江区三模)小华同学在做“测定小灯泡的电功率”实验中,电源电压为6伏且保持不变,待测小灯泡标有“3.8伏”字样.所用器材齐全完好,有2个不同规格的滑动变阻器A和B,变阻器A标有“20欧 2安”的字样,变阻器B标有“5欧 3安”的字样.
(2013?松江区三模)小华同学在做“测定小灯泡的电功率”实验中,电源电压为6伏且保持不变,待测小灯泡标有“3.8伏”字样.所用器材齐全完好,有2个不同规格的滑动变阻器A和B,变阻器A标有“20欧 2安”的字样,变阻器B标有“5欧 3安”的字样. (2013?松江区三模)某兴趣小组在“研究物体吸收热量的多少与哪些因素有关”的实验中,提出了以下几种猜想:
(2013?松江区三模)某兴趣小组在“研究物体吸收热量的多少与哪些因素有关”的实验中,提出了以下几种猜想: