题目内容
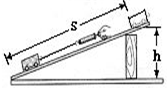 如图所示,在探究斜面机械效率的实验中,把木块沿斜面匀速拉动时,测得数据如下表:
如图所示,在探究斜面机械效率的实验中,把木块沿斜面匀速拉动时,测得数据如下表:| 木块的重力G/N | 斜面的高度h/m | 沿斜面的拉力F/N | 斜面长s/m |
| 10 | 1 | 3 | 5 |
66.67%
66.67%
.(2)画出木块所受力的示意图.
(3)摩擦是影响斜面机械效率的重要因素,把物体拉上斜面,就要克服物体和斜面间的摩擦力作额外功.如果斜面光滑程度相同,请对下面两个问题做出正确判断,并从物体受力情况的变化来分析影响斜面机械效率的原因
①如果斜面长度相同而高度增大,机械效率怎样变化?为什么?
②如果斜面高度相同而长度增大,机械效率怎样变化?为什么?
分析:(1)根据表中实验数据,由功的计算公式W=Fs求出有用功与总功,然后由效率公式求出斜面的机械效率.
(2)对木块受力分析,从力的作用点,沿力的方向作有向线段,即可作出物体受力的示意图.
(3)根据具体情景,分析克服摩擦力所做的额外功如何变化,然后得出结论.
(2)对木块受力分析,从力的作用点,沿力的方向作有向线段,即可作出物体受力的示意图.
(3)根据具体情景,分析克服摩擦力所做的额外功如何变化,然后得出结论.
解答:解:(1)有用功W=Gh=10N×1m=10J,
总功W总=Fs=3N×5m=15J,
斜面的机械效率:
η=
×100%=
×100%≈66.67%.
(2)匀速拉动木块向上运动时,
木块受竖直向下的重力G、平行于斜面向上的拉力F、平行于斜面向下的摩擦力f、垂直于斜面向上的支持力N,
从木块的重心,沿各力的方向作有向线段,
作出各力的示意图,木块受力示意图如图所示:
(3)①斜面长度相同而高度增大时,
木块受到的摩擦力减少,由于斜面长度不变,
则克服摩擦力做的额外功减少;
斜面的高度增大,有用功W=Gh增大,
有用功增大,而额外功减小,斜面的机械效率增大.
②如果斜面高度相同,有用功W=Gh不变;
斜面的长度增大,克服摩擦力做的额外功增大;
总功等于有用功与额外功之和,总功增大,
有用功不变,总功变大,则斜面的机械效率减小.
故答案为:(1)66.67%;(2)木块受力示意图如图所示.
(3)①机械效率增大;因为克服摩擦力所做的额外功减小;
②机械效率减小;因为克服摩擦力所做的额外功增加.
总功W总=Fs=3N×5m=15J,
斜面的机械效率:
η=
| W |
| W总 |
| 10J |
| 15J |
(2)匀速拉动木块向上运动时,

木块受竖直向下的重力G、平行于斜面向上的拉力F、平行于斜面向下的摩擦力f、垂直于斜面向上的支持力N,
从木块的重心,沿各力的方向作有向线段,
作出各力的示意图,木块受力示意图如图所示:
(3)①斜面长度相同而高度增大时,
木块受到的摩擦力减少,由于斜面长度不变,
则克服摩擦力做的额外功减少;
斜面的高度增大,有用功W=Gh增大,
有用功增大,而额外功减小,斜面的机械效率增大.
②如果斜面高度相同,有用功W=Gh不变;
斜面的长度增大,克服摩擦力做的额外功增大;
总功等于有用功与额外功之和,总功增大,
有用功不变,总功变大,则斜面的机械效率减小.
故答案为:(1)66.67%;(2)木块受力示意图如图所示.
(3)①机械效率增大;因为克服摩擦力所做的额外功减小;
②机械效率减小;因为克服摩擦力所做的额外功增加.
点评:本题考查了求斜面的机械效率、作木块受力示意图、分析斜面高度或长度变化时,斜面的机械效率如何变化等问题,
熟练应用功的计算公式、效率公式、掌握作力的示意图的方法、会判断克服摩擦力所做额外功的多少,即可正确解题.
熟练应用功的计算公式、效率公式、掌握作力的示意图的方法、会判断克服摩擦力所做额外功的多少,即可正确解题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图所示,在探究“斜面的机械效率”的实验中,以下说法正确的是( )
如图所示,在探究“斜面的机械效率”的实验中,以下说法正确的是( ) (2012?襄城区模拟)如图所示,在探究“斜面的机械效率”的实验中,以下说法错误的是( )
(2012?襄城区模拟)如图所示,在探究“斜面的机械效率”的实验中,以下说法错误的是( ) 如图所示,在探究“斜面的机械效率”的实验中,测斜面的机械效率的实验中:
如图所示,在探究“斜面的机械效率”的实验中,测斜面的机械效率的实验中: 如图所示,在探究“斜面的机械效率”的实验中,测斜面的机械效率的实验中:
如图所示,在探究“斜面的机械效率”的实验中,测斜面的机械效率的实验中: