Question

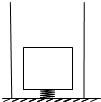（2013?丰台区二模）如图所示，用质量不计、长度为10cm的弹簧将边长为10cm的正方体物块的下表面与底面积为200cm²的圆柱形容器底部相连，正方体物块竖直压在弹簧上且不与容器壁接触，此时弹簧的长度缩短为2cm；然后向容器内部缓慢倒入水（水不溢出），当弹簧的长度恰好恢复到原长时停止倒水；现将一小铁块轻压在正方体物块上，此时正方体物块刚好没入水中，则铁块的质量为

0.3

kg．已知：弹簧弹力F与其长度的改变量x的关系式为F=x×100N/m上述过程中弹簧始终在竖直方向伸缩，且撤去其所受力后，弹簧可以恢复原长．不计弹簧的体积及其所受的浮力，取g=10N/kg．

Answer 1

分析：（1）首先根据原来弹簧的缩短量结合F=x×100N/m计算出物块的重力G；
（2）根据倒入水后弹簧的长度恰好恢复到原长得知物块受到的浮力与其重力相等，从而根据公式V排=

F浮

ρ水g

计算出此时物块浸入水中的体积和深度；
（3）现将一小铁块轻压在正方体物块上，此时正方体物块刚好没入水中，计算出此时弹簧缩短的长度，以物块和铁块组成的整体为研究对象进行受力分析，根据平衡关系得出铁块的重力，从而计算出其质量．

解答：解：当不倒水时，物块受力如图所示：

则G=F₁=x₁×100N/m=（10-2）×10^-2m×100N/m=8N；
倒入水后，弹簧恢复原长，则F_浮=G=8N，
根据F_浮=ρ_水gV_排得，V_排=

F浮

ρ水g

=

8N

1.0×103kg/m3×10N/kg

=8×10^-4m³；
所以物体浸入水中的深度h=

V排

S

=

8×10-4m3

10×10×10-4m2

=0.08m；
由题意知，物体全部浸没时，F_浮′=ρ_水gV_排′=1.0×10³kg/m³×10N/kg×（0.1m）³=10N；
物体浸入水中的深度增加了0.02m，
当在物块上面加铁块，在物块下降的同时水面会上升，又因为物块的底面积为100cm²，容器的底面积为200cm²，所以物体周围的面积为200cm²-100cm²=100cm²，则物块下降的距离与水面上升的距离相等，因此弹簧的长度减小了x₂=

1

2

×0.02m=0.01m；
此时弹簧对物块的支持力为F₂=x₂×100N/m=0.01m×100N/m=1N；
以物块和铁块组成的整体为研究对象进行受力分析，如图所示：

则F_浮′+F₂=G+G_铁，
则G_铁=F_浮′+F₂-G=10N+1N-8N=3N；
则m_铁=

G铁

g

=

3N

10N/kg

=0.3kg．
故答案为：0.3．

点评：此题考查了有关浮力的计算，要掌握阿基米德原理，并能对公式进行变形，对各种情况进行正确地受力分析，得出物块完全浸没时弹簧缩短的长度是此题的难点，总之此题的综合性较强，难度较大．