题目内容
如图装置为某学生在科技创新大赛时发明的可以直接测量密度的“密度天平”。其制作过程如下:选择一根长1米杠杆,调节两边螺母使杠杆在水平位置平衡。在左侧离中点10厘米的A位置用细线固定一个质量为150克、容积为80毫升的容器。右侧用细线悬挂一质量为50克钩码(细线的质量忽略不计)。测量时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位置直接读出液体的密度。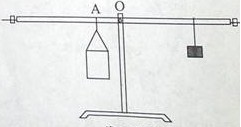
(1)该“密度天平”的“零刻度”应标在右端离支点O cm处。
(2)该“密度天平”的量程为多大?
(3)若将钩码的质量适当增大,该“密度天平”的量程将 (选填“增大”、“减小”或“不变”).
(1)30 (2)1.25g/cm3 (3)增大
解析试题分析:本题中的密度天平是利用了杠杆平衡原理,当左边小桶内不放物体时,杠杆在水平位置平衡,钩码所对应的位置就是0刻度线所在的位置。
根据杠杆平衡条件F1L1=F2L2,150g×10cm="50g×L" 2,则L2=30cm
所以此密度天平的零刻度线所在位置距O点30cm处。
密度天平的量程是指当钩码移至最右端时容器内液体的密度,只要求出此时小桶内液体的质量即可。
当钩码位于最右端时,L2’=50cm,再次利用杠杆平衡条件m×10cm=50g×50cm,则m=250g
桶内液体的质量为100g,液体的密度为
若将钩码的质量适当增大,则杠杆右侧的力和力臂乘积会增大,小桶能装的液体质量也变大,则能测的液体的密度也会变大。
考点:杠杆平衡条件的应用

 名校课堂系列答案
名校课堂系列答案小华和小红在广场看到小朋友玩套圈游戏(如图甲所示)时,发现水平抛出的套圈落地时的水平距离不尽相同,引起了他们的思考.于是他们按图乙所示方法,找来圆弧轨道(末端水平)、一个小钢球,探究钢球水平抛出的落地点到抛出点的水平距离与哪些因素有关.探究前,他们提出了如下猜想: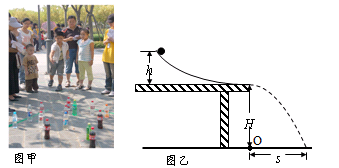
猜想1:与小球在轨道上静止释放时的高度h有关;
猜想2:与水平抛出点的离地高度H有关.
(1)为了验证猜想是否正确,需用测量水平距离s.请你运用学过的物理知识帮助他们确定s的起点位置O,写出具体的方法 .
(2)下表是他们在实验中测得的数据:
①分析实验序号为 的数据,可得出的初步结论是:在其它条件相同的情况下, 与小球在轨道上静止释放时的高度h成正比;
②综合分析表中所给数据,请你写出s与h、H之间的关系式: .
③接着小华又想探究小球抛出的水平距离与小球的质量是否有关.请你简述小华的实验方案.简要做法: ;如何判断: .
| 实验 序号 | 轨道末端水平部分离地面的高度 H/m | 小球在轨道上由静止释放时的高度h/m | 落地点与抛出 点的水平距离s/m | 落地点与抛出 点的水平距离的平方s2/m2 |
| 1 | 0.5 | 0.1 | 0.45 | 0.2 |
| 2 | 0.5 | 0.2 | 0.63 | 0.4 |
| 3 | 0.5 | 0.3 | 0.78 | 0.6 |
| 4 | 1.0 | 0.1 | 0.63 | 0.4 |
| 5 | 1.0 | 0.2 | 0.89 | 0.8 |
| 6 | 1.0 | 0.3 | 1.10 | 1.2 |
随着我国经济的不断增长,国防力量也在加强,我国第一艘航空母舰“辽宁号”已正式交接.根据某航母的主要参数值列式计算:(g=10N/kg,ρ海水=1.03×103kg/m3)
| 主要参数值 | |
| 航母总质量(包括舰载飞机) | 6×107kg |
| 每架舰载飞机的质量 | 5150kg |
| 每架舰载飞机与甲板的总接触面积 | 5000cm2 |
| 航母正常航行速度 | 54km/h |
| 航母以正常航行速度行驶时所受阻力 | 3.6×108N |
(2)求航母所受的总重力和浮力的大小.
(3)若航母以正常航行速度匀速从甲地开往乙地,行驶了540km.求此过程中航母牵引力的功率.
(4)若其中一架舰载飞机起飞后,求航母排开海水的体积减少了多少?
下列说法中正确的是
| A.零下18℃的液体能发生汽化现象 |
| B.发生扩散现象的原因是由于分子不停地做无规则运动 |
| C.把红墨水滴入热水中的扩散实验中,我们会看到红墨水的分子在运动 |
| D.由于液体和气体能够流动,而固体不能流动,所以固体分子是静止的 |

