Question

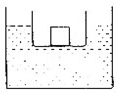（2010?房山区一模）如图所示，柱形容器中装有密度为ρ₁=1.2g/cm³的某种液体，将一金属块放入底面积为S=100cm²的长方体塑料盒中，塑料盒竖直漂浮在液面上，且液体不会溢出容器，其浸入液体的深度为h₁=20cm．若把金属块从塑料盒中取出，用细线系在塑料盒的下方，刚入该液体中，塑料盒竖直漂浮在液面上，且金属块不接触容器底，塑料盒浸入液体的深度为h₂=15cm．剪断细线，金属块沉到容器底部，塑料盒仍然竖直漂浮在液面上，其浸入液体的深度为h₃=10cm．则金属块的密度ρ₂=

2.4

g/cm³．

Answer 1

分析：根据物体漂浮时，浮力等于重力，物体在塑料盒内和用细线系在塑料盒下时都是漂浮，所以受到的浮力相等，根据两种情况下排开液体的体积相等，计算出物体的体积；
根据物体与塑料盒漂浮时排开液体的体积计算出金属盒和金属块的总重力；根据塑料盒漂浮时排开液体的体积，计算出塑料盒的重力，从而可以计算出金属盒的重力；
根据ρ=

m

V

=

G

gV

计算出金属块的密度．

解答：解：以金属块和塑料盒组成的整体为研究对象，当金属块放入塑料盒内时：
G_总=F_浮1=ρ₁gSh₁=1.2×10³kg/m³×10N/kg×100×20×10^-6m³=24N；
若把金属块用细线系在塑料盒的下方，此时金属块和塑料盒仍漂浮，浮力仍等于金属盒和塑料盒的总重力，浮力不变，因此排开液体的体积不变，则：
V_金=Sh₁-Sh₂=100×20×10^-6m³-100×15×10^-6m³=5×10^-4m³；
塑料盒的重力G_塑=F_浮2=ρ₁gSh₃=1.2×10³kg/m³×10N/kg×100×10×10^-6m³=12N；
则金属块的重力G_金=G_总-G_塑=24N-12N=12N；
所以ρ₂=

m金

V金

=

G金

gV金

=

12N

10N/kg×5×10-4m3

=2.4×10³kg/m³=2.4g/cm³；
故答案为：2.4．

点评：此题考查了有关物体密度的计算，主要需应用阿基米德原理，及物体漂浮时浮力与重力相等，根据已知条件确定金属块的体积和质量是解决此题的关键．