如图所示.一轻质杠杆支在支架上.OA= 20cm, G1为边长是5cm的正方体.G2重为20N.当OC=l0cm时.绳子的拉力为 N.此时G1对地面的压强为2×104Pa.现用一水平拉力.使G2以 cm/s的速度向右匀速运动.经过12.5s后.可使G1对地面的压力恰好为0. 题目和参考答案——青夏教育精英家教网—

题目内容

如图所示，一轻质杠杆支在支架上，OA="20cm," G₁为边长是5cm的正方体，G₂重为20N。当OC=l0cm时，绳子的拉力为 N，此时G₁对地面的压强为2×10⁴Pa。现用一水平拉力，使G₂以 cm/s的速度向右匀速运动，经过12.5s后，可使G₁对地面的压力恰好为0。

10 4

解析试题分析：根据杠杆的平衡条件可求G₁对A点的拉力大小为：，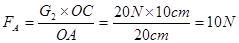
G₁的底面积为5cm×5cm=25cm²=2.5×10^-3m²，
所以根据压强公式得G₁对地面的压力为：F=pS=2×10⁴Pa×2.5×10^-3m²=50N，
所以物体G₁的重力为G₁= F+F_A=50N+10N=60N；
当G₁对地面的压力为0，即A点的拉力等于G₁重力60N，
根据杠杆的平衡条件可得的G₂的力臂为，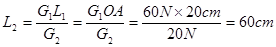
所以物体G₂移动的距离为s=L₂-OC=60cm-10cm=50cm，
所以物体G₂移动的速度为。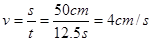
考点：杠杆的平衡条件速度公式的应用二力平衡的应用

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

有一质地均匀的实心圆柱体，重5N，高10cm．将它挂在弹簧测力计下，然后竖直浸入到装有足够多水的容器中，当它刚好完全浸没时，弹簧测力计示数为3N，如图所示．g取10N/kg，求此时

（1）圆柱体所受到的浮力大小；
（2）圆柱体下表面所受到水的压强；
（3）圆柱体的密度．

如图所示为我国首辆 “玉兔号”月球车。登月前，在水平地面上进行了测试，月球车匀速直线行驶180 m用时60min，若车的质量为140kg，受到地面的摩擦阻力为500N，网状轮子与地面接触的总面积为0.02m²。求：

（1）月球车受到的重力；
（2）月球车对水平地面的压强；
（3）月球车在测试过程中的功率。

图所示是一辆新型坦克，其质量为20t，发动机的额定功率为1000kW，每条履带与水平地面的接触面积为2m²。g取10N/kg，求：

（1）坦克的重力。
（2）坦克静止时对水平地面的压强；
（3）坦克以额定功率行驶10min，发动机所做的功。

如图所示是某型号的电动巡逻车，其主要技术参数如表所示。已知两名巡警的总质量为120kg共同乘坐该车。在水平路面上以最高时速行驶10min。求：

（1）巡逻车10min行驶的路程是多少？
（2）该车前挡风玻璃采用一种新型的防弹玻璃，此种玻璃轻巧、硬度大，测得玻璃的长1.5m、宽1m、厚0.4cm，查得此种玻璃的密度是2×10³kg/m³，这块玻璃的质量是多大？
（3）若轮胎与地面的总接触面积是8×10^－2m2，巡逻车停止时，人和车对水平地面的压强是多大？（g取10N／kg）
（4）电动巡逻车和普通汽车比有什么优点？（写一条即可）

如图所示，是我国88式主战坦克，重40t，高2m，每条履带与地面的接触面积2m²，该坦克具有潜渡功能．请解答下列问题：

（1）该坦克在水平路面上行驶时，对地面的压强为多大？
（2）若坦克在深为5m的河流中潜渡时，坦克对水平河床的压力为10⁵N，则该坦克的体积为多大？
（3）坦克在该河流中潜渡时，在坦克顶部面积为0.8m²的舱门受到水的压力为多大？

（多选）关于晶体和非晶体，下列说法中不正确的是（）
A晶体和非晶体都有固定的熔点
B．晶体和非晶体吸收热量时都可能变成液体
C．晶体和非晶体熔化时都要吸收热量且温度保持不变
D．非晶体熔化时要先变软，然后变成粘稠体，最后变成液体。

2014年2月4日温州很多地区下冰雹，冰雹形成原因比较复杂，其中一种原因是液态水因气温骤降而形成的。比较大的冰雹会砸破车窗、砸伤行人，给人民群众的人身财产安全造成危害。请回答下列问题：
（1）液态水变成冰雹的物态变化名称是     ，这个过程要放出热量。
（2）比较大的冰雹会砸破车窗、砸伤行人，说明下落的冰雹具有     能。
（3）有一颗冰雹质量为100克，从1000米的高空下落到地面（假设冰雹在下落过程中质量不变）,重力做功     焦。

下列科学方法中，错误的是（　　）

A．找出蒸发和沸腾的异同点，运用了类比法

B．根据变为原来的压强的方法想到减小压强的方法，运用了逆向思考法

C．两个5Ω的电阻串联与一个10Ω的电阻效果相同，运用了等效法

D．研究牛顿第一定律时，在斜面小车实验基础上，通过理想化推理得到结论，运用了逐渐逼近法

试题分类