题目内容
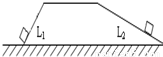
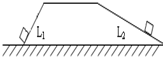 一个重为G的物体分别沿如图所示的左右两个斜面,被推上同一个平台,如果沿两个斜面推动物体时所受摩擦力一样大,那么两个斜面相比( )
一个重为G的物体分别沿如图所示的左右两个斜面,被推上同一个平台,如果沿两个斜面推动物体时所受摩擦力一样大,那么两个斜面相比( )分析:斜面倾斜角度越大,越费力.左斜面的倾斜角度大于右斜面,据此判断哪一边更省力;
沿两个斜面推动物体时所受摩擦力一样大,L1<L2,根据W额=fL得出利用两个斜面做额外功的大小关系,而有用功相同,可得总功大小关系,最后利用效率公式判断效率大小关系.
沿两个斜面推动物体时所受摩擦力一样大,L1<L2,根据W额=fL得出利用两个斜面做额外功的大小关系,而有用功相同,可得总功大小关系,最后利用效率公式判断效率大小关系.
解答:解:∵左斜面倾斜角度大于右斜面,
∴用右斜面更省力;
由题知,沿两个斜面推动物体时所受摩擦力一样大,f1=f2,L1<L2,
∵W额=fL,
∴利用两个斜面做额外功:W额1<W额2,
∵W有用=Gh,G、h相同,
∴利用两个斜面做的有用功:W有用1=W有用2,
∵W总=W有用+W额,
∴利用两个斜面做的总功:W总1<W总2,
∵η=
,
∴利用两个斜面的效率η1>η2.
由上述分析可知,用左斜面省力少,机械效率比右高.
故选A.
∴用右斜面更省力;
由题知,沿两个斜面推动物体时所受摩擦力一样大,f1=f2,L1<L2,
∵W额=fL,
∴利用两个斜面做额外功:W额1<W额2,
∵W有用=Gh,G、h相同,
∴利用两个斜面做的有用功:W有用1=W有用2,
∵W总=W有用+W额,
∴利用两个斜面做的总功:W总1<W总2,
∵η=
| W有用 |
| W总 |
∴利用两个斜面的效率η1>η2.
由上述分析可知,用左斜面省力少,机械效率比右高.
故选A.
点评:本题考查斜面的省力情况、有用功、额外功、总功、机械效率的大小比较,关键是知道沿两个斜面推动物体时所受摩擦力一样大,从而得出额外功的大小关系.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目


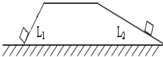 一个重为G的物体分别沿如图所示的左右两个斜面,被推上同一个平台,如果沿两个斜面推动物体时所受摩擦力一样大,那么两个斜面相比
一个重为G的物体分别沿如图所示的左右两个斜面,被推上同一个平台,如果沿两个斜面推动物体时所受摩擦力一样大,那么两个斜面相比