题目内容
将一正方体挂在弹簧测力计下,其示数为G,当物体的一半浸没在水中,弹簧测力计示数24N,物体排开水的质量为0.8kg,则G=
31.84N
31.84N
,物体的密度为2.03×103kg/m3
2.03×103kg/m3
.当物体全部浸没在某种液体中时,测力计的示数为19.2N.则液体的密度为0.8×103kg/m3
0.8×103kg/m3
.若将物体放在水平桌面上,物体受到的支持力是32N
32N
.分析:(1)知道物体排开水的质量为0.8kg,求出物体排开水的重力,即物体受到水的浮力,根据浸入水中弹簧测力计的示数,利用称重法求物体重力;
(2)根据物体受到的浮力,利用阿基米德原理求物体的体积;求出石块的质量,利用密度公式ρ=
求物体的密度;
(3)利用称重法求物体受到某种液体的浮力,再利用阿基米德原理求某种液体的密度.
(4)物体放在水平桌面上,根据物体受力平衡判断.
(2)根据物体受到的浮力,利用阿基米德原理求物体的体积;求出石块的质量,利用密度公式ρ=
| m |
| V |
(3)利用称重法求物体受到某种液体的浮力,再利用阿基米德原理求某种液体的密度.
(4)物体放在水平桌面上,根据物体受力平衡判断.
解答:解:
(1)∵物体排开水的质量为0.8kg,则根据阿基米德原理知:F浮=G排=m排g=0.8kg×9.8N/kg=7.84N;
∴物体的重力为:G=F浮+F示=7.84N+24N=31.84N;
(2)∵F浮=ρ水V排g,
∴排开水的体积:
V排=
=
=8×10-4m3,
∵是物体的一半浸没在水中,
∴物体体积为:V=2V排=2×8×10-4m3=1.6×10-3m3,
又因m=
=
=3.25kg,
物体的密度:
ρ=
=
≈2.03×103kg/m3;
(3)物体在某种液体中时受到的浮力:
F浮′=G-F′=31.84N-19.2N=12.64N,
∵F浮′=ρ液V排′g,
∴ρ液=
=
≈0.81×103kg/m3.
(4)若将物体放在水平桌面上,物体受到的支持力与重力是一对平衡力,则N=G=31.84N.
故答案为:31.84N;2.03×103kg/m3;0.81×103kg/m3;31.84N.
(1)∵物体排开水的质量为0.8kg,则根据阿基米德原理知:F浮=G排=m排g=0.8kg×9.8N/kg=7.84N;
∴物体的重力为:G=F浮+F示=7.84N+24N=31.84N;
(2)∵F浮=ρ水V排g,
∴排开水的体积:
V排=
| m排 |
| ρ水 |
| 0.8kg |
| 1×103kg/m3 |
∵是物体的一半浸没在水中,
∴物体体积为:V=2V排=2×8×10-4m3=1.6×10-3m3,
又因m=
| G |
| g |
| 31.84N |
| 9.8N/kg |
物体的密度:
ρ=
| m |
| V |
| 3.25kg |
| 1.6×10-3m3 |
(3)物体在某种液体中时受到的浮力:
F浮′=G-F′=31.84N-19.2N=12.64N,
∵F浮′=ρ液V排′g,
∴ρ液=
| F浮′ |
| V排′g |
| 12.64N |
| 1.6×10-3m3×9.8N/kg |
(4)若将物体放在水平桌面上,物体受到的支持力与重力是一对平衡力,则N=G=31.84N.
故答案为:31.84N;2.03×103kg/m3;0.81×103kg/m3;31.84N.
点评:称重法的运用是本题中求浮力的基本方法,本题的难点还是两次浮力公式的运用,利用物体排开水的体积与排开液体的体积关系,进而求出液体的密度.

练习册系列答案
相关题目
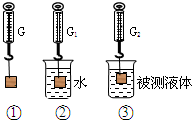 璐璐根据学到的浮力知识,设计了一个测量液体密度的实验,如图所示,将一物体挂在弹簧测力计下,分别浸没在水中和被测液体中.若图1中弹簧测力计的示数为G,图2中弹簧测力计的示数为G1,图3中弹簧测力计的示数为G2,水的密度用ρ水表示,则被测液体的密度表达式为ρ=
璐璐根据学到的浮力知识,设计了一个测量液体密度的实验,如图所示,将一物体挂在弹簧测力计下,分别浸没在水中和被测液体中.若图1中弹簧测力计的示数为G,图2中弹簧测力计的示数为G1,图3中弹簧测力计的示数为G2,水的密度用ρ水表示,则被测液体的密度表达式为ρ=