题目内容
将标有“3V 3W”的灯L1和标有“6V 4W”的灯L2串联(灯泡电阻不变),现要使其中一盏灯长时间正常发光,则电源电压是
8
8
V,电路的总功率是5.3
5.3
W.若将这两个电阻并联在某电路中,要使电路长时间工作,干路中最大的电流是1.3
1.3
A,电源的最大电压是3
3
V.分析:由灯泡的铭牌可求额定电流和电阻,两灯泡串联时只有一盏灯正常发光说明电路中的电流为两灯泡额定电流最小的那个,根据电阻的串联和欧姆定律求出电路中的总电压,根据P=UI求出该电路消耗的总功率;两灯泡并联时,根据并联电路的电压特点可知并联电路的最大电压选两者最小的额定电压,根据欧姆定律求出各支路电流,利用并联电路的电流特点求出干路电流.
解答:解:两灯泡的额定电流分别为:
I1=
=
=1A,I2=
=
=
A,
两灯泡的电阻:
R1=
=
=3Ω,R2=
=
=9Ω,
(1)∵串联时只有一盏灯正常发光,
∴电路中的电流为两灯泡额定电流最小的一个,即I=
A,
两灯泡两端的电压:
U=I(R1+R2)=
A×(3Ω+9Ω)=8V,
该电路消耗的总功率:
P=UI=8V×
A≈5.3W;
(2)∵两灯泡并联时只有一盏灯泡正常发光,
∴并联电路的电压为额定电压最小的一个,即U=3V,通过L1的电流为I1=1A,
通过L2的电流I2′=
=
≈0.3A,
干路电流I=I1+I2′=1A+0.3A=1.3A.
故答案为:8;5.3;1.3;3.
I1=
| P1 |
| U1 |
| 3W |
| 3V |
| P2 |
| U2 |
| 4W |
| 6V |
| 2 |
| 3 |
两灯泡的电阻:
R1=
| U1 |
| I1 |
| 3V |
| 1A |
| U2 |
| I2 |
| 6V | ||
|
(1)∵串联时只有一盏灯正常发光,
∴电路中的电流为两灯泡额定电流最小的一个,即I=
| 2 |
| 3 |
两灯泡两端的电压:
U=I(R1+R2)=
| 2 |
| 3 |
该电路消耗的总功率:
P=UI=8V×
| 2 |
| 3 |
(2)∵两灯泡并联时只有一盏灯泡正常发光,
∴并联电路的电压为额定电压最小的一个,即U=3V,通过L1的电流为I1=1A,
通过L2的电流I2′=
| U |
| R2 |
| 3V |
| 9Ω |
干路电流I=I1+I2′=1A+0.3A=1.3A.
故答案为:8;5.3;1.3;3.
点评:本题考查了串联电路的电流特点和串联电路的电压特点以及欧姆定律、电功率公式的灵活应用,关键是知道两灯泡并联时电路中的最大电流为最小的额定电流,并联时电路中的最大电压为最小的额定电压.

练习册系列答案
相关题目
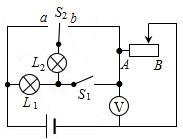 在如图所示的电路中,电源电压为3V,L1上标有“6V 3W”,L2上标有“3V 3W”,滑动变阻器上标有“10Ω 1.5A”.要使L2正常发光,则应使S1、S2分别处于
在如图所示的电路中,电源电压为3V,L1上标有“6V 3W”,L2上标有“3V 3W”,滑动变阻器上标有“10Ω 1.5A”.要使L2正常发光,则应使S1、S2分别处于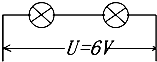 现有标有“6V 3W”字样的灯泡L1和标有“3V 3W”字样的灯泡L2;将两灯泡串联接入到电压为6V的电源上(如图),求:
现有标有“6V 3W”字样的灯泡L1和标有“3V 3W”字样的灯泡L2;将两灯泡串联接入到电压为6V的电源上(如图),求: