题目内容
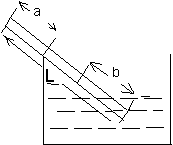
 有一根长为l的均匀细棒,一部分浸入密度为ρ的液体中,长度为b,另一端搁在容器壁上,伸出器壁的长度为a,如图所示.则细棒的密度等于
有一根长为l的均匀细棒,一部分浸入密度为ρ的液体中,长度为b,另一端搁在容器壁上,伸出器壁的长度为a,如图所示.则细棒的密度等于
- A.ρ?
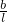 (1+
(1+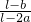 )
) - B.ρ?
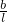 (1-
(1-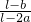 )
) - C.ρ?
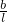 (1+
(1+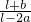 )
) - D.ρ?
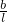 (1+
(1+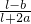 )
)
A
分析:对细棒进行受力分析:细棒除受器壁对它的支持力外,还受重力和浮力.若把细棒看作能绕器壁搁置点O处转动的杠杆,那么就必须确定重力和浮力的大小、方向和作用点,然后,再根据杠杆的平衡条件列等式求解.
解答:因重力的作用点在物体的重心,由于棒是均匀的,所以重力的作用点A在棒的中心;又因细棒只有浸入液体中的部分b才受浮力,所以浮力的作用点B在浸入部分的中点.如图所示

设均匀细棒的横截面积为S,则其重力为G=ρglS.根据阿基米德原理,浸入液体中部分受到的浮力F浮=ρ′gV排=ρ′gbS
由图可知,OA=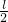 -a,OB=l-a-
-a,OB=l-a-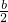 ,又设重力和浮力的力臂分别为l1、l2,则根据相似三角形的性质得:OA:OB=l1:l2.
,又设重力和浮力的力臂分别为l1、l2,则根据相似三角形的性质得:OA:OB=l1:l2.
由杠杆的平衡条件得:Gl1=F浮l2,
即ρ′glS(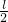 -a)=ρgbS(l-a-
-a)=ρgbS(l-a-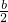 )
)
将上式整理后得:ρ′=ρ?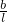 (1+
(1+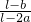 )
)
故选A.
点评:本题综合考查杠杆平衡条件以及物体受力分析的应用,该题关键是重力和浮力的作用点应确定在何处,难度较大.
分析:对细棒进行受力分析:细棒除受器壁对它的支持力外,还受重力和浮力.若把细棒看作能绕器壁搁置点O处转动的杠杆,那么就必须确定重力和浮力的大小、方向和作用点,然后,再根据杠杆的平衡条件列等式求解.
解答:因重力的作用点在物体的重心,由于棒是均匀的,所以重力的作用点A在棒的中心;又因细棒只有浸入液体中的部分b才受浮力,所以浮力的作用点B在浸入部分的中点.如图所示

设均匀细棒的横截面积为S,则其重力为G=ρglS.根据阿基米德原理,浸入液体中部分受到的浮力F浮=ρ′gV排=ρ′gbS
由图可知,OA=
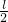 -a,OB=l-a-
-a,OB=l-a-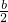 ,又设重力和浮力的力臂分别为l1、l2,则根据相似三角形的性质得:OA:OB=l1:l2.
,又设重力和浮力的力臂分别为l1、l2,则根据相似三角形的性质得:OA:OB=l1:l2.由杠杆的平衡条件得:Gl1=F浮l2,
即ρ′glS(
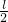 -a)=ρgbS(l-a-
-a)=ρgbS(l-a-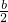 )
)将上式整理后得:ρ′=ρ?
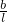 (1+
(1+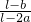 )
) 故选A.
点评:本题综合考查杠杆平衡条件以及物体受力分析的应用,该题关键是重力和浮力的作用点应确定在何处,难度较大.

练习册系列答案
相关题目
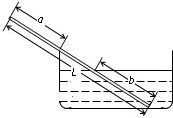 有一根长为l的均匀细棒,一部分浸入密度为ρ的液体中,长度为b,另一端搁在容器壁上,伸出器壁的长度为a,如图所示.则细棒的密度等于( )
有一根长为l的均匀细棒,一部分浸入密度为ρ的液体中,长度为b,另一端搁在容器壁上,伸出器壁的长度为a,如图所示.则细棒的密度等于( )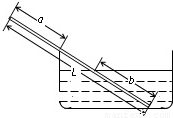
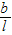 (1+
(1+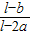 )
)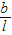 (1-
(1-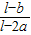 )
)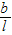 (1+
(1+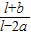 )
)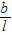 (1+
(1+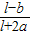 )
)