题目内容
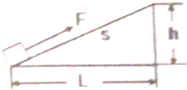 (2013?乌鲁木齐)小明在探究“斜面的机械效率”的实验中,用长度S=0.50m的木板搭成一个斜面,用弹簧测力计将重力G=5.0N的物块从斜面底端匀速拉至斜面顶端.
(2013?乌鲁木齐)小明在探究“斜面的机械效率”的实验中,用长度S=0.50m的木板搭成一个斜面,用弹簧测力计将重力G=5.0N的物块从斜面底端匀速拉至斜面顶端.(1)小明在实验中,调整斜面的高度为h=0.22m,将物块从斜面底端匀速拉至顶端的过程中,弹簧测力计的示数F=4.0N,则有用功为
1.1
1.1
J,机械效率为55%
55%
.(2)小明利用上述器材进一步研究发现,木板搭成倾角不同的斜面时,将物块从斜面底端匀速拉至斜面顶端的过程中,额外功W额外与斜面的水平长度L(木板在水平面上的正投影长度)有如下关系:
| L(m) | 0.45 | 0.40 | 0.35 | 0.30 |
| W额外(J) | 0.90 | 0.80 | 0.70 | 0.60 |
正
正
比,小明查阅资料后证实此结论是正确的.根据此结论,当斜面的水平长度L=0.40m时,斜面的机械效率为65.2%
65.2%
;当木板平放在水平桌面上,水平匀速拉动木板上的物块时,弹簧测力计的示数为2
2
N.分析:(1)由功的计算公式求出有用功与总功,然后由效率公式求出斜面的效率.
(2)分析表中实验数据,得出额外功与斜面水平长度的关系;
根据斜面的长度与斜面水平长度,由勾股定理求出斜面的高度,
然后由功的公式求出有用功与总功,由效率公式求出斜面的效率;
当木板放在水平面上时,克服摩擦力做的功为额外功,
根据额外功与斜面水平长度的关系求出斜面水平时的额外功,
由功的公式求出摩擦力,然后由平衡条件求出弹簧测力计的拉力.
然后由功的计算公式求出.
(2)分析表中实验数据,得出额外功与斜面水平长度的关系;
根据斜面的长度与斜面水平长度,由勾股定理求出斜面的高度,
然后由功的公式求出有用功与总功,由效率公式求出斜面的效率;
当木板放在水平面上时,克服摩擦力做的功为额外功,
根据额外功与斜面水平长度的关系求出斜面水平时的额外功,
由功的公式求出摩擦力,然后由平衡条件求出弹簧测力计的拉力.
然后由功的计算公式求出.
解答:解:(1)有用功W有用=Gh=5N×0.22=1.1J,
总功W总=Fs=4N×0.5m=2J,
斜面的效率η=
=
=55%;
(2)由表中实验数据可知,W额外与L成正比;
当斜面的水平长度L=0.40m时,
斜面高度h′=
=
=0.3m,
此时有用功W有用′=Gh′=5N×0.3m=1.5J,
总功W总′=W有用′+W额外=1.5J+0.80J=2.3J,
效率η′=
=
=65.2%;
当木板平放在水平桌面上,斜面的水平长度L=S=0.50m,
设此时的额外功为W,则
=
,W=1J,
∵W=fS,∴f=
=
=2N,
物体做匀速运动,由平衡条件得:
弹簧测力计的拉力F=f=2N;
故答案为:(1)1.1;55%;(2)正;65.2%;2.
总功W总=Fs=4N×0.5m=2J,
斜面的效率η=
| W有用 |
| W总 |
| 1.1J |
| 2J |
(2)由表中实验数据可知,W额外与L成正比;
当斜面的水平长度L=0.40m时,
斜面高度h′=
| S2-L2 |
| (0.5m)2-(0.4m)2 |
此时有用功W有用′=Gh′=5N×0.3m=1.5J,
总功W总′=W有用′+W额外=1.5J+0.80J=2.3J,
效率η′=
| W有用′ |
| W总′ |
| 1.5J |
| 2.3J |
当木板平放在水平桌面上,斜面的水平长度L=S=0.50m,
设此时的额外功为W,则
| 0.45m |
| 0.90J |
| 0.50m |
| W |
∵W=fS,∴f=
| W |
| S |
| 1J |
| 0.50m |
物体做匀速运动,由平衡条件得:
弹簧测力计的拉力F=f=2N;
故答案为:(1)1.1;55%;(2)正;65.2%;2.
点评:本题考查了求斜面效率、实验数据分析、求拉力等问题,有一定的难度;掌握功的计算公式、效率公式、总功与有用功与额外功间的关系即可正确解题.

练习册系列答案
相关题目