��Ŀ����
��2012?��������ģ����ͼ��ʾ��һ����10m��ϸ�����ȵĽ���·�Ƹˣ�����ˮƽ�����ϣ�������ֱ��������F1������������ˣ�ʹ·�Ƹ˵�A��ǡ���뿪����ʱ���˶Ե����ѹ��ΪN1����������������·�Ƹ˵Ĺ����У�������Ļ�еЧ�ʱ��ֲ���Ϊ��1�����ù�����ֱ��������F2���һ���������ˣ�ʹ·�Ƹ˵�B��ǡ���뿪����ʱ���˶Ե����ѹ��ΪN2����������������·�Ƹ˵Ĺ����У�������Ļ�еЧ�ʱ��ֲ���Ϊ��2��N1��N2=4��5��F1��F2=9��5����1����2=10��9��ÿ���������ؾ�Ϊ50N������������ء������쳤�������Ħ�����Ժ��ԣ�g=10N/kg��
��1��������G����
��2��·�Ƹ���G����
��3�����ػ���·�Ƹ˱���ˮƽ״̬����ʱ������Ӧϵ�ںδ���
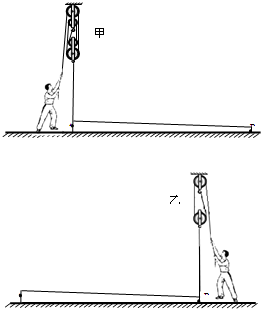
��1��������G����
��2��·�Ƹ���G����
��3�����ػ���·�Ƹ˱���ˮƽ״̬����ʱ������Ӧϵ�ںδ���

��������1�����ˡ��������Լ��ܸ�Ϊ�о��������������������������Ӧ��ͼʾ�����ܵ���ֱ���µ���������ֱ���ϵ�֧�������������������ܵ���ֱ���ϵ���������ֱ���µ��������������ã����ݸܸ�ƽ��������г���ϵʽ��
��2���ˡ����ֶ�����ƽ��״̬����˸���ƽ�������ص㡢�ܸ�ƽ��������ֱ��ʾ���ˡ������Լ��ܸ��ܵ������Ĺ�ϵʽ�������ݦ�=
��ʾ��������Ļ�еЧ�ʣ�
��3������֪������AB=10m�� G��=100N�� G��=50N�� N1��N2=4��5��F1��F2=9��5����1����2=10��9�������г��Ĺ�ϵʽ�У���֮���������������G����·�Ƹ���G���Լ��ܸ˵����ģ�
��2���ˡ����ֶ�����ƽ��״̬����˸���ƽ�������ص㡢�ܸ�ƽ��������ֱ��ʾ���ˡ������Լ��ܸ��ܵ������Ĺ�ϵʽ�������ݦ�=
| Fh |
| (F+G)nh |
��3������֪������AB=10m�� G��=100N�� G��=50N�� N1��N2=4��5��F1��F2=9��5����1����2=10��9�������г��Ĺ�ϵʽ�У���֮���������������G����·�Ƹ���G���Լ��ܸ˵����ģ�
����⣺������������ͼ��ʾ��
�ü�������A�ˣ�
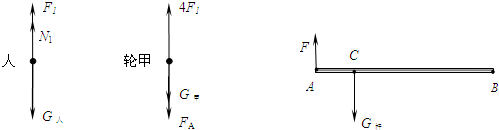
���һ�������B�ˣ�
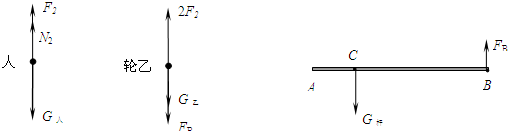
�ü�������A��ʱ�Ĺ�ϵʽ��
G��=F1+N1 ����
4F1=��FA+G��������
FA��AB=G����CB����
��1=
=
����
���һ�������B��ʱ�Ĺ�ϵʽ��
G��=F2+N2 ����
2F2=��FB+G���� ����
FB��AB=G������AB-CB�� ����
��2=
=
����
�ɢ٢ݿɵã�
=
=
����
�ɢڢɵã�
=
=
����
�ɢܢ�ɵã�
=
��
=
����11��
��AB=10m��G��=100N��G��=50N��������ʽ
��֮��G��=625N��G��=1000N��AC=2m�����轫·�Ƹ˱���ˮƽ״̬����ʱ����Ӧϵ�ھ�A��2m����
�𣺣�1��������625N��
��2��·�Ƹ���1000N��
��3�����ػ���·�Ƹ˱���ˮƽ״̬����ʱ������Ӧϵ�ھ�A��2m����
�ü�������A�ˣ�
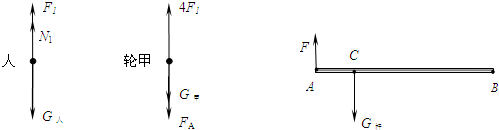
���һ�������B�ˣ�
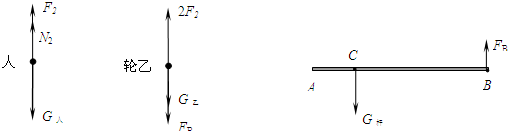
�ü�������A��ʱ�Ĺ�ϵʽ��
G��=F1+N1 ����
4F1=��FA+G��������
FA��AB=G����CB����
��1=
| FAh |
| (FA+G��)h |
| FAh |
| 4F1h |
���һ�������B��ʱ�Ĺ�ϵʽ��
G��=F2+N2 ����
2F2=��FB+G���� ����
FB��AB=G������AB-CB�� ����
��2=
| FBh |
| (FB+G��)h |
| FBh |
| 2F2h |
�ɢ٢ݿɵã�
| N1 |
| N2 |
| G��-F1 |
| G��-F2 |
| 4 |
| 5 |
�ɢڢɵã�
| F1 |
| F2 |
| FA+G�� |
| 2(FB+G��) |
| 9 |
| 5 |
�ɢܢ�ɵã�
| ��1 |
| ��2 |
| FA |
| FB |
| F2 |
| 2F1 |
| 10 |
| 9 |
��AB=10m��G��=100N��G��=50N��������ʽ
��֮��G��=625N��G��=1000N��AC=2m�����轫·�Ƹ˱���ˮƽ״̬����ʱ����Ӧϵ�ھ�A��2m����
�𣺣�1��������625N��
��2��·�Ƹ���1000N��
��3�����ػ���·�Ƹ˱���ˮƽ״̬����ʱ������Ӧϵ�ھ�A��2m����
�������������ۺ��Ժ�ǿ����Ŀ��������������ʽ����еЧ�ʹ�ʽ��ƽ��״̬���ж��Լ��ܸ�ƽ�������������ؼ���һ����ȷ�����������������Ǹ���ͼʾ����������֪ʶ�г���ϵʽ��Ȼ���֮���ɣ�

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
�����Ŀ
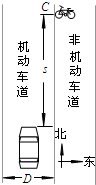 ��2012?��������ģ����ͼ��ʾ��һ���γ��ڻ�����������������v=54km/h������ʻ����֪���������Ŀ���D=3m���γ�����3m������1.4m��������ʻ�нγ�ʼ��λ�ڻ������������м䣮��һ�������г����ٺᴩ������������֪���г���1.8m��ǰ�������ǻ�������������������紦��C��ʱ��γ����ϱ�����ľ���s=12m������˫����û�в�ȡ�κδ�ʩ�����г��ٶ�����Ϊ
��2012?��������ģ����ͼ��ʾ��һ���γ��ڻ�����������������v=54km/h������ʻ����֪���������Ŀ���D=3m���γ�����3m������1.4m��������ʻ�нγ�ʼ��λ�ڻ������������м䣮��һ�������г����ٺᴩ������������֪���г���1.8m��ǰ�������ǻ�������������������紦��C��ʱ��γ����ϱ�����ľ���s=12m������˫����û�в�ȡ�κδ�ʩ�����г��ٶ�����Ϊ