题目内容
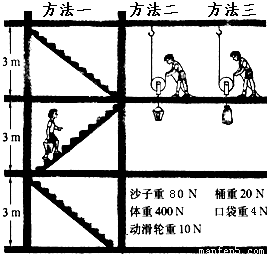
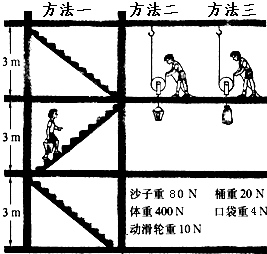要把沙子运上三楼，小慧采用了图中的第一种方法，1min完成了任务．若不计摩擦，试求：（1）小慧的功率；
（2）小慧运沙子时的机械效率；
（3）哪种方法的机械效率最大，为什么？
分析：（1）图中的第一种方法，小慧做的总功是克服沙子和桶和自身重力做的功，根据W=Gh求出小慧做的功，利用P=
求出功率；
（2）小会对沙子做的功为有用功，根据W=Gh求出其大小，再利用效率公式求出慧运沙子时的机械效率；
（3）在有用功相同的情况下，额外功越少的，其机械效率一定越高．
| W |
| t |
（2）小会对沙子做的功为有用功，根据W=Gh求出其大小，再利用效率公式求出慧运沙子时的机械效率；
（3）在有用功相同的情况下，额外功越少的，其机械效率一定越高．
解答：解：（1）图中的第一种方法，
小慧做的总功：
W总=G总h=（80N+20N+400N）×6m=3000J，
小慧的功率：
P=
=
=50W；
（2）小慧运沙子时的有用功：
W有=G沙h=80N×6m=480J，
运沙子时的机械效率：
η=
=
=16%；
（3）三种方法的最终目的都是要将80N的沙子提升6m，因此，其有用功是相同的；
第三次用的口袋最轻，所以第三次做的额外功最少，利用机械做的总功最小，故其机械效率最高．
答：（1）小慧的功率为50W；
（2）小慧运沙子时的机械效率为16%；
（3）方法三的机械效率最大，原因是：有用功相同，额外功最少．
小慧做的总功：
W总=G总h=（80N+20N+400N）×6m=3000J，
小慧的功率：
P=
| W总 |
| t |
| 3000J |
| 60s |
（2）小慧运沙子时的有用功：
W有=G沙h=80N×6m=480J，
运沙子时的机械效率：
η=
| W有 |
| W总 |
| 480J |
| 3000J |
（3）三种方法的最终目的都是要将80N的沙子提升6m，因此，其有用功是相同的；
第三次用的口袋最轻，所以第三次做的额外功最少，利用机械做的总功最小，故其机械效率最高．
答：（1）小慧的功率为50W；
（2）小慧运沙子时的机械效率为16%；
（3）方法三的机械效率最大，原因是：有用功相同，额外功最少．
点评：本题的关键是要知道，运上三楼，高度只有两层楼高，在上楼梯过程中，人的重力在重力方向上也通过了距离，故人也要克服自身的重力做功．
练习册系列答案
能考试全能100分系列答案
相关题目
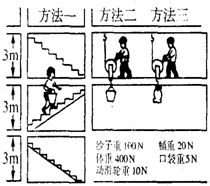要把重100N的沙子运上三楼，小明采用了图中的第一种方法，1min完成了任务．若不计摩擦，试求：
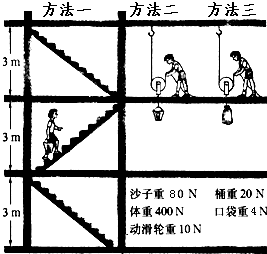要把沙子运上三楼，小慧采用了图中的第一种方法，1min完成了任务．若不计摩擦，试求：
