题目内容
L是标有“6V 3W“的电灯，电压是8伏特的电源求：电阻R和滑动变阻器RW的阻值各是多大时，才能使滑动变阻器的滑片P无论在什么位置上，加在电灯两端的电压都不超过3～6伏特的范围．
分析：已知灯泡的额定功率和额定电压，并且加在灯泡两端的电压都不超过3-6V的范围，所以要利用灯泡两端最小电压和最大电压值，列出两个等量关系式，求出相关的两个未知量即可．
解答：解：灯泡的电阻灯R灯=
=
=12Ω；
根据灯泡两端电压的最大值6V和最小值3V列两个关系式：
当滑动变阻器的阻值为零时：6V=
×12Ω ①
当滑动变阻器的阻值最大时：3V=
×12Ω ②
由①②可得：R=4Ω，R′=16Ω；
答：电阻和滑动变阻器的阻值各是4Ω，16Ω时，才能使滑片P无论在什么位置上，加在灯泡两端的电压都不超过3-6V的范围．
| U2 |
| P |
| (6V)2 |
| 3W |
根据灯泡两端电压的最大值6V和最小值3V列两个关系式：
当滑动变阻器的阻值为零时：6V=
| 8V |
| 12Ω+R |
当滑动变阻器的阻值最大时：3V=
| 8V |
| 12Ω+R+R′ |
由①②可得：R=4Ω，R′=16Ω；
答：电阻和滑动变阻器的阻值各是4Ω，16Ω时，才能使滑片P无论在什么位置上，加在灯泡两端的电压都不超过3-6V的范围．
点评：本题关键是要找到做题的等量关系，只要找到等量关系，利用相关公式，列出二元一次方程组，题目便可解出．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
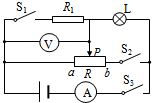（2008?丰台区二模）如图所示电路，电源电压保持不变，L是标有“6V 3W”的小灯泡，R是滑动变阻器．闭合开关S3，断开开关S1、S2，滑片P位于中点时，灯泡L恰好正常发光，电压表V的示数为U1；当S1、S2都闭合，滑片P滑至b端时，电流表示数为1.5A，电压表V的示数为U2；U1：U2=1：2，下列选项正确的是（ ）
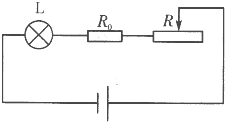（2008?徐州）在如图所示电路中，L是标有“6V 3W”字样的小电灯，它与定值电阻R．和滑动变阻器R组成串联电路，电源电压保持8V不变．无论变阻器滑片怎样移动，小电灯两端电压都不超过3V～6V的范围．忽略温度变化对灯丝电阻的影响，求：
（2011?北京二模）如图所示电路，电源是多档的学生电源，L是标有“6V 3W”的小灯泡，R2是滑动变阻器，R1是定值电阻．当电源位于第一档，只闭合开关S，调节滑动变阻器的滑片P处于a点时，灯泡正常发光，电压表的示数是4V，滑动变阻器的功率是Pa；当电源位于第二档，只闭合开关S，调节滑动变阻器的滑片P处于b点时，电压表的示数是3.2V，滑动变阻器的功率是Pb，灯泡的功率PL′是额定功率的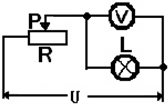
如图所示，电路两端的电压U=6V且保持不变．L是标有“6V 3W”的灯泡，它的电阻不随温度变化．滑动变阻器的滑片位于某一位置时，电压表的示数为U1，滑动变阻器消耗的电功率为P1；移动滑片到另一位置时，电压表的示数为U2，滑动变阻器消耗的功率为P2．要使U2=2U1，P2=P1滑动变阻器的总电阻至少是多少欧？