题目内容
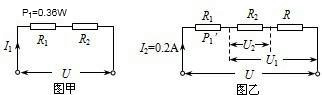
 (2008?丰台区一模)如图所示,电源电压一定,R1和R2为两个未知阻值的定值电阻,R是滑动变阻器,闭合开关S1、S2后,R1消耗的实际电功率P1为0.36W;闭合开关S1、断开S2,滑动变阻器的滑片P移到最右端时,R1消耗的实际电功率为P1?,P1:P1?=9:1,此时电流表读数为0.2A,电压表V1、V2的读数分别为U1和U2,U1:U2=7:2,
(2008?丰台区一模)如图所示,电源电压一定,R1和R2为两个未知阻值的定值电阻,R是滑动变阻器,闭合开关S1、S2后,R1消耗的实际电功率P1为0.36W;闭合开关S1、断开S2,滑动变阻器的滑片P移到最右端时,R1消耗的实际电功率为P1?,P1:P1?=9:1,此时电流表读数为0.2A,电压表V1、V2的读数分别为U1和U2,U1:U2=7:2,求(1)R1的阻值;
(2)电路中消耗的最小电功率.
分析:画出开关S1、S2都闭合时和开关S1闭合、S2断开时,滑动变阻器的滑片P置于最右端时的等效电路图;
(1)先根据已知R1消耗的实际电功率之比求出图乙中消耗的电功率,然后利用P=I2R求出R1的阻值.
(2)根据P=
可知,当电路中电阻最大即开关S1闭合、S2断开时,滑动变阻器的滑片P置于R最右端时电路消耗的电功率最小;先利用图甲、图乙中R1消耗的实际电功率和P=I2R求出两电路图的电流关系,再利用电源的电压不变和欧姆定律表示出电阻之间的关系,根据电压表的示数和欧姆定律表示出电阻关系,联立方程得出电阻的大小;最后利用电阻的串联特点和P=I2R求出电路中消耗的最小电功率.
(1)先根据已知R1消耗的实际电功率之比求出图乙中消耗的电功率,然后利用P=I2R求出R1的阻值.
(2)根据P=
| U2 |
| R |
解答:解:当开关S1、S2都闭合时,电路如图甲所示;
当开关S1闭合、S2断开时,滑动变阻器的滑片P置于最右端时,电路如图乙所示.
(1)∵P1:P1?=9:1,P1=0.36W,
∴P1?=0.04W,
∵P=I2R
∴R1=
=
=1Ω;
(2)当开关S1闭合、S2断开时,滑动变阻器的滑片P置于R最右端时,电路总电阻最大,消耗的电功率最小.
由图甲、图乙中R1消耗的实际电功率和P=I2R可知,
=
=9:1,得
=3:1,
∵电源的电压不变,
∴
=
=3:1---------①
=
=7:2-------②
由①②两式得:R2=4R1=4Ω,R=
R2=10Ω;
R总=R1+R2+R=1Ω+4Ω+10Ω=15Ω,
Pmin=
R总=(0.2A)2×15Ω=0.6W.
答:(1)R1的阻值为1Ω;
(2)电路中消耗的最小电功率0.6W.
当开关S1闭合、S2断开时,滑动变阻器的滑片P置于最右端时,电路如图乙所示.

(1)∵P1:P1?=9:1,P1=0.36W,
∴P1?=0.04W,
∵P=I2R
∴R1=
| P1′ | ||
|
| 0.04W |
| (0.2A)2 |
(2)当开关S1闭合、S2断开时,滑动变阻器的滑片P置于R最右端时,电路总电阻最大,消耗的电功率最小.
由图甲、图乙中R1消耗的实际电功率和P=I2R可知,
| ||
|
| P1 |
| P1′ |
| I1 |
| I2 |
∵电源的电压不变,
∴
| I1 |
| I2 |
| R1+R2+R |
| R1+R2 |
| U1 |
| U2 |
| R2+R |
| R2 |
由①②两式得:R2=4R1=4Ω,R=
| 5 |
| 2 |
R总=R1+R2+R=1Ω+4Ω+10Ω=15Ω,
Pmin=
| I | 2 2 |
答:(1)R1的阻值为1Ω;
(2)电路中消耗的最小电功率0.6W.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的计算,关键是公式及其变形式的灵活运用,难点是根据已知条件找出两种情况的联系建立方程进行求解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 (2008?丰台区一模)在图中画出合适的透镜.
(2008?丰台区一模)在图中画出合适的透镜. (2008?丰台区一模)如图,物体A重120N,在重力为GB的物体B的作用下在水平桌面上做匀速直线运动,A与桌面之间的摩擦力为f.如果在A上加一个水平向左大小为180N的拉力F,物体B匀速上升,则下列选项正确的是( )(不计摩擦、绳重及滑轮重)
(2008?丰台区一模)如图,物体A重120N,在重力为GB的物体B的作用下在水平桌面上做匀速直线运动,A与桌面之间的摩擦力为f.如果在A上加一个水平向左大小为180N的拉力F,物体B匀速上升,则下列选项正确的是( )(不计摩擦、绳重及滑轮重)