题目内容
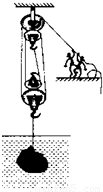
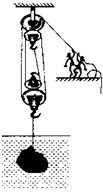 产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求:
产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求:
(1)石头的重力;(2)石头的体积;(3)拉力所做的功.
解:(1)石头出水后,
∵F= G石,
G石,
∴G石=4F2=4×7.0×103N=2.8×104N;
(2)石头在出水前:
∵F1= (G石-F浮)
(G石-F浮)
∴F浮=G石-4F1=2.8×104N-4×4.5×103N=1.0×104N,
∵F浮=ρ水v排g=ρ水v石g,
∴石头的体积:
v石=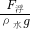 =
=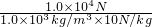 =1m3,
=1m3,
(3)石头在出水前,拉力移动的距离:
s1=4h1=4×5m=20m,
W1=F1×s1=4.5×103N×20m=9×104J,
石头出水后,拉力移动的距离:
s2=4h2=4×1m=4m,
W2=F2×s2=7.0×103N×4m=2.8×104J,
拉力做的总功:
W总=W1+W2=9×104J+2.8×104J=1.18×105J.
答:(1)石头的重力为2.8×104N;
(2)石头的体积为1m3;
(3)拉力所做的功为1.18×105J.
分析:由滑轮组的结构可以看出,承担物重的绳子股数n=4,则s=4h.
(1)知道石头出水后人的拉力,不计摩擦及动滑轮重,利用F= G石求拉力大小;
G石求拉力大小;
(2)知道石头在出水前人的拉力,不计摩擦及动滑轮重,利用F= F拉=
F拉= (G石-F浮)求石头的浮力,再根据阿基米德原理求排开水的体积(石头的体积);
(G石-F浮)求石头的浮力,再根据阿基米德原理求排开水的体积(石头的体积);
(3)根据s=4h求出石头在水面下、水面上,拉力移动的距离,利用W=Fs求出两种情况下拉力做的功,再计算拉力做的总功.
点评:本题考查了学生对功的公式、阿基米德原理、使用滑轮组拉力的计算,确认n的大小(直接从动滑轮上引出的绳子股数)是解题的突破口,利用好不计摩擦及动滑轮重时拉力F= G这个关系.
G这个关系.
∵F=
 G石,
G石,∴G石=4F2=4×7.0×103N=2.8×104N;
(2)石头在出水前:
∵F1=
 (G石-F浮)
(G石-F浮)∴F浮=G石-4F1=2.8×104N-4×4.5×103N=1.0×104N,
∵F浮=ρ水v排g=ρ水v石g,
∴石头的体积:
v石=
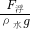 =
=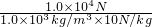 =1m3,
=1m3,(3)石头在出水前,拉力移动的距离:
s1=4h1=4×5m=20m,
W1=F1×s1=4.5×103N×20m=9×104J,
石头出水后,拉力移动的距离:
s2=4h2=4×1m=4m,
W2=F2×s2=7.0×103N×4m=2.8×104J,
拉力做的总功:
W总=W1+W2=9×104J+2.8×104J=1.18×105J.
答:(1)石头的重力为2.8×104N;
(2)石头的体积为1m3;
(3)拉力所做的功为1.18×105J.
分析:由滑轮组的结构可以看出,承担物重的绳子股数n=4,则s=4h.
(1)知道石头出水后人的拉力,不计摩擦及动滑轮重,利用F=
 G石求拉力大小;
G石求拉力大小;(2)知道石头在出水前人的拉力,不计摩擦及动滑轮重,利用F=
 F拉=
F拉= (G石-F浮)求石头的浮力,再根据阿基米德原理求排开水的体积(石头的体积);
(G石-F浮)求石头的浮力,再根据阿基米德原理求排开水的体积(石头的体积);(3)根据s=4h求出石头在水面下、水面上,拉力移动的距离,利用W=Fs求出两种情况下拉力做的功,再计算拉力做的总功.
点评:本题考查了学生对功的公式、阿基米德原理、使用滑轮组拉力的计算,确认n的大小(直接从动滑轮上引出的绳子股数)是解题的突破口,利用好不计摩擦及动滑轮重时拉力F=
 G这个关系.
G这个关系. 
练习册系列答案
相关题目
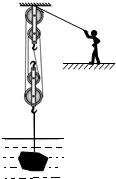 (2005?河池)产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求:
(2005?河池)产自我市的岩滩红水河奇石闻名全国乃至世界,采石工人用如图所示的装置将一块奇石从5m深的水底提升到离水面1m高的船上.已知石头在出水前人的拉力F1=4.5×103N,石头出水后人的拉力F2=7.0×103N,不计摩擦及动滑轮重,g取10N/kg,求: